题目内容
12.已知点P(-4t,t)在角α的终边上,且α∈(0,π),求$\frac{sinα•(1-ta{n}^{2}α)}{\frac{1}{cosα}}$的值.分析 由条件利用任意角的三角函数的定义求得sinα、cosα的值,再化简所给的式子,可得结果.
解答 解:由点P(-4t,t)在角α的终边上,且α∈(0,π),可得t>0,x=-4t,y=t,r=|OP|=$\sqrt{17}$t,
∴cosα=$\frac{x}{r}$=$\frac{-4t}{\sqrt{17}t}$=-$\frac{4}{\sqrt{17}}$,sinα=$\frac{y}{r}$=$\frac{t}{\sqrt{17}t}$=$\frac{1}{\sqrt{17}}$,
∴$\frac{sinα•(1-ta{n}^{2}α)}{\frac{1}{cosα}}$=sinαcosα•$\frac{{cos}^{2}α{-sin}^{2}α}{{cos}^{2}α}$=$\frac{sinα{(cos}^{2}α{-sin}^{2}α)}{cosα}$=$\frac{\frac{1}{\sqrt{17}}(\frac{16}{17}-\frac{1}{17})}{\frac{-4}{\sqrt{17}}}$=-$\frac{15}{68}$.
点评 本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
4.若函数y=f(x-1)的图象过点(2,3),则( )
| A. | f(2)=3 | B. | f(3)=2 | C. | f(1)=3 | D. | f(3)=1 |
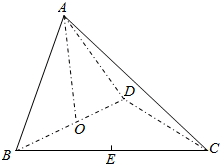 如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.
如图,在三棱锥A-BCD中,O,E分别是BD,BC的中点,CA=CB=CD=BD=2,AB=AD=$\sqrt{2}$.