题目内容
18．
把正整数数列的所有数按照从小到大的原则写成如图所示的数表，第k行有k个数，第k行的第s个数（从左数起）记为A（k，s），则2015这个数可记为A（63，62）．
分析 根据第k行有k个数，可知每行数的个数成等差数列，进而分析每一行最后一个数字与行数的关系，可得答案．
解答 解：由第k行有k个数，知每一行数的个数构成等差数列，首项是1，公差是1，
∴前n行共有1+2+3+…+n=$\frac{n（n+1）}{2}$个数，
∴即第n行的最后一个数字为$\frac{n（n+1）}{2}$，
当n=62时，$\frac{n（n+1）}{2}$=1953，
当n=63时，$\frac{n（n+1）}{2}$=2016，
故2015在第63行，由2015-1953=62得，
2015为第63行的第62个数字，
故2015这个数可记为A（63，62），
故答案为：A（63，62）
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
相关题目
8．已知椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1，F2，过右焦点F2作x轴的垂线，交椭圆于A，B两点．若等边△ABF1的周长为$4\sqrt{3}$，则椭圆的方程为（ ）
| A． | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | B． | $\frac{x^2}{3}+\frac{y^2}{6}=1$ | C． | $\frac{x^2}{2}+\frac{y^2}{3}=1$ | D． | $\frac{x^2}{9}+\frac{y^2}{4}=1$ |
9．函数y=sin2x+cos2x的值域是（ ）
| A． | [-1，1] | B． | [-2，2] | C． | [-1，$\sqrt{2}$] | D． | [-$\sqrt{2}$，$\sqrt{2}$] |
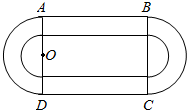某学校要建造一个面积为10000平方米的运动场．如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成．跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮．已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元．
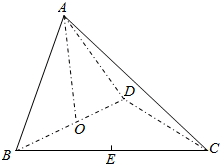如图，在三棱锥A-BCD中，O，E分别是BD，BC的中点，CA=CB=CD=BD=2，AB=AD=$\sqrt{2}$．
8．已知x、y的取值如表所示：
若从散点图分析，y与x线性相关，且线性回归直线方程为$\widehat{y}$=0.95x+$\widehat{a}$，则$\widehat{a}$的值等于2.6．
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |