题目内容
已知椭圆E:
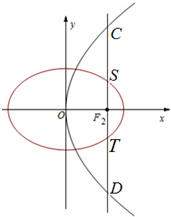
+y2=1的左、右顶点分别为A、B,圆x2+y2=4上有一动点P,P在x轴上方,C(1,0),直线PA交椭圆E于点D,连结DC,PB.
(Ⅰ)若∠ADC=90°,求△ADC的面积S;
(Ⅱ)设直线PB,DC的斜率存在且分别为k1,k2,若k1=2k2,求λ的取值范围.
| x2 |
| 4 |
(Ⅰ)若∠ADC=90°,求△ADC的面积S;
(Ⅱ)设直线PB,DC的斜率存在且分别为k1,k2,若k1=2k2,求λ的取值范围.
(Ⅰ)设D(x0,y0),
∵椭圆E:
+y2=1的左、右顶点分别为A(-2,0)、B(2,0),
C(1,0),∠ADC=90°,
∴
•
=(x0+2,y0)•(x0-1,y0)=(x0+2)(x0-1)+y02=0,
联立
,
解得
或
(舍),
∴S△ADC=
×3×
=
,
∴△ADC的面积S为
.
(Ⅱ)设P(x1,y1),D(x2,y2),∵P,Q分别在圆与椭圆上,
∴x12+y12=4,
+y22=1,
∵A(-2,0),P(x1,y1),D(x2,y2)三点共线,
则有
=
.
∵k1=
,k2=
,又k1=λk2,即
=λ•
,
∴
•
=λ•
•
,即
=λ•
,
又y12=4-x12,y22=1-
,代入得-1=λ•
,
即λ=
=4(1-
),
∵x2∈(-2,2),∴λ<3,又∵λ≠0,
∴λ∈(-∞,0)∪(0,3).
∵椭圆E:
| x2 |
| 4 |
C(1,0),∠ADC=90°,
∴
| AD |
| AC |
联立
|
解得
|
|
∴S△ADC=
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
∴△ADC的面积S为
| 2 |
(Ⅱ)设P(x1,y1),D(x2,y2),∵P,Q分别在圆与椭圆上,
∴x12+y12=4,
| x22 |
| 4 |
∵A(-2,0),P(x1,y1),D(x2,y2)三点共线,
则有
| y1 |
| x1+2 |
| y2 |
| x2+2 |
∵k1=
| y1 |
| x1-2 |
| y2 |
| x2-1 |
| y1 |
| x1-2 |
| y2 |
| x2-1 |
∴
| y1 |
| x1-2 |
| y1 |
| x1+2 |
| y2 |
| x2-1 |
| y2 |
| x2+2 |
| y12 |
| x12-4 |
| y22 |
| (x2-1)(x2+2) |
又y12=4-x12,y22=1-
| x22 |
| 4 |
1-
| ||
| (x2-1)(x2+2) |
即λ=
| 4(1-x2) |
| 2-x2 |
| 1 |
| 2-x2 |
∵x2∈(-2,2),∴λ<3,又∵λ≠0,
∴λ∈(-∞,0)∪(0,3).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目