题目内容

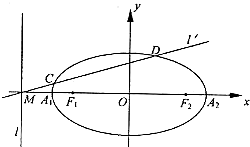
已知椭圆的中心在坐标原点，焦点F1、F2在x轴上，长轴A1A2的长为4，左准线l与x轴的交点为M，
MA1
=2
A1F1
．
（I）求椭圆的标准方程；
（Ⅱ）过点M的直线l'与椭圆交于C、D两点，若
OC
•
OD
=0，求直线l'的方程．
（I）设椭圆的方程为
x2
a2
+
y2
b2
=1(a＞b＞0)，半焦距为c
则|
MA1
|=
a2
c
-a，|
A1F1
|=a-c.
由题意，得
a2
c
-a=2(a-c)
2a=4
a2=b2+c2
∴a=2，b=
3
，c=1
故所求椭圆方程为
x2
4
+
y2
3
=1

（II）点M的坐标为M（-4，0），设C、D两点坐标分别为C（x1，y1），D（x2，y2），l'的方程为y=k（x+4），代入椭圆方程整理，得
(3+4k2)x2+32k2x+64k2-12=0
则x1+x2=-
32k2
3+4k2
，x1x2=
64k2-12
3+4k2
由
OC
•
OD
=0得x1x2+y1y2=0
又y1y2=k2[x1x2+4(x1+x2)+16]
后三个式子得(1+k2)
64k2-12
3+4k2
+4k2
(-32k2)
3+4k2
+16k2=0
解得k2=
3
25
，代入第一个中检验有△＞0，∴k=±
3
5
，
所以所求直线l’的主程为y=±
3
5
(x+4)
练习册系列答案
相关题目
已知椭圆E：
x2
4
+y2=1的左、右顶点分别为A、B，圆x2+y2=4上有一动点P，P在x轴上方，C（1，0），直线PA交椭圆E于点D，连结DC，PB．
（Ⅰ）若∠ADC=90°，求△ADC的面积S；
（Ⅱ）设直线PB，DC的斜率存在且分别为k1，k2，若k1=2k2，求λ的取值范围．
若椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点分别为F1，F2，线段F1F2被抛物线y2=2bx的焦点F内分成了3：1的两段．
（1）求椭圆的离心率；
（2）过点C（-1，0）的直线l交椭圆于不同两点A、B，且
AC
=2
CB
，当△AOB的面积最大时，求直线l和椭圆的方程．
已知两点F′（-2，0），F（2，0），点P为坐标平面内的动点，且满足|
F′F
||
FP
|+
F′F
•
F′P
=0．
（1）求动点P（x，y）的轨迹C的方程；
（2）过点F的直线l与轨迹C和⊙F：（x-2）2+y2=1交于四点，自下而上依次记这四点为A、B、C、D，求
AB
•
CD
的最小值．
已知椭圆G：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
6
3
，右焦点为（2
2
，0），斜率为1的直线l与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3，2）．
（Ⅰ）求椭圆G的方程；
（Ⅱ）求△PAB的面积．
过抛物线y2=2px焦点F作直线l交抛物线于A，B两点，O为坐标原点，则△ABO为（　　）
A．锐角三角形B．直角三角形C．不确定D．钝角三角形
已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左右焦点为F1（-c，0），F2（c，0），点Q是椭圆外的动点，满足|
F1Q
|=2a，点P是线段F1Q与该椭圆的交点
（1）若点P的横坐标为
a
2
，证明：|
F1P
|=a+
c
2

（2）若存在点Q，使得△F1QF2的面积等于b2，求椭圆离心率的取值范围．
已知F1，F2分别为椭圆C1：
x2
b2
+
y2
a2
=1（a＞b＞0）的上下焦点，其F1是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF2|=
3
5
．
（1）试求椭圆C1的方程；
（2）与圆x2+（y+1）2=1相切的直线l：y=k（x+t）（t≠0）交椭圆于A，B两点，若椭圆上一点P满足
OA
+
OB
=λ
OP
，求实数λ的取值范围．
已知椭圆G：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
1
2
，过椭圆G右焦点F的直线m：x=1与椭圆G交于点M（点M在第一象限）．
（Ⅰ）求椭圆G的方程；
（Ⅱ）已知A为椭圆G的左顶点，平行于AM的直线l与椭圆相交于B，C两点．判断直线MB，MC是否关于直线m对称，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网