题目内容
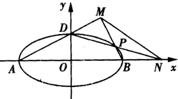
已知抛物线C1:y2=8x与双曲线C2:
-
=1(a>0,b>0)有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
(1)求双曲线C2的方程;
(2)以双曲线C2的另一焦点F1为圆心的圆M与直线y=
x相切,圆N:(x-2)2+y2=1.过点P(1,
)作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t,问:
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求双曲线C2的方程;
(2)以双曲线C2的另一焦点F1为圆心的圆M与直线y=
| 3 |
| 3 |
| s |
| t |
(1)∵抛物线C1:y2=8x的焦点为F2(2,0),
∴双曲线C2的焦点为F1(-2,0)、F2(2,0),…(1分)
设A(x0,y0)在抛物线C1:y2=8x上,且|AF2|=5,
由抛物线的定义得,x0+2=5,
∴x0=3,∴y02=8×3=24,∴y0=2
,…(3分)
∴|AF1|=
=7,…(4分)
又∵点A在双曲线C2上,由双曲线定义得:
2a=|7-5|=2,∴a=1,∴双曲线C2的方程为:x2-
=1.…(6分)
(2)
为定值.下面给出说明.
设圆M的方程为:(x+1)2+y2=r2,
∵圆M与直线y=
x相切,
∴圆M的半径为r=
=
,
∴圆M:(x+2)2+y2=3.…(7分)
当直线j1的斜率不存在时不符合题意,…(8分)
设l1的方程为y-
=k(x-1),即kx-y+
-k=0,
设l2的方程为y-
=-
(x-1),即x+ky-
k-1=0,
∴点F1到直线l1的距离为d1=
,
点F2到直线l2的距离为d2=
,…(10分)
∴直线l1被圆M截得的弦长:
S=2
=2
,…(11分)
直线l2被圆N截得的弦长t=2
=2
,…(12分)
∴
=
=
=
,
∴
为定值
.…(13分)
∴双曲线C2的焦点为F1(-2,0)、F2(2,0),…(1分)
设A(x0,y0)在抛物线C1:y2=8x上,且|AF2|=5,
由抛物线的定义得,x0+2=5,
∴x0=3,∴y02=8×3=24,∴y0=2
| 6 |
∴|AF1|=
(3+2)2+(±2
|
又∵点A在双曲线C2上,由双曲线定义得:
2a=|7-5|=2,∴a=1,∴双曲线C2的方程为:x2-
| y2 |
| 3 |
(2)
| s |
| t |
设圆M的方程为:(x+1)2+y2=r2,
∵圆M与直线y=
| 3 |
∴圆M的半径为r=
2
| ||||
|
| 3 |
∴圆M:(x+2)2+y2=3.…(7分)
当直线j1的斜率不存在时不符合题意,…(8分)
设l1的方程为y-
| 3 |
| 3 |
设l2的方程为y-
| 3 |
| 1 |
| k |
| 3 |
∴点F1到直线l1的距离为d1=
|3k-
| ||
|
点F2到直线l2的距离为d2=
|
| ||
|
∴直线l1被圆M截得的弦长:
S=2
3-(
|
|
直线l2被圆N截得的弦长t=2
1-(
|
|
∴
| S |
| t |
|
=
|
| 3 |
∴
| S |
| t |
| 3 |

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目