题目内容
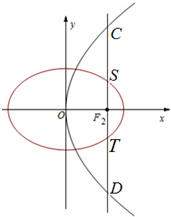
如图,椭圆E:
+
=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线l与椭圆交于S、T两点,与抛物线交于C、D两点,且
=2
.
(Ⅰ)求椭圆E的方程;
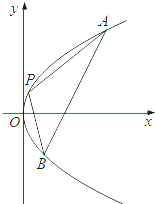
(Ⅱ)若过点M(2,0)的直线与椭圆E相交于两点A,B,设P为椭圆E上一点,且满足
+
=t
(O为坐标原点),当|
-
|<
时,求实数t的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| |CD| |
| |ST| |
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆E相交于两点A,B,设P为椭圆E上一点,且满足
| OA |
| OB |
| OP |
| PA |
| PB |
2
| ||
| 3 |

(Ⅰ)由抛物线方程,得焦点F2(1,0).
所以椭圆E的方程为:
+
=1.
解方程组
得C(1,2),D(1,-2).
由于抛物线、椭圆都关于x轴对称,
∴
=
=2
,|F2S|=
,∴S(1,
).
因此,
+
=1,解得b2=1并推得a2=2.
故椭圆的方程为
+y2=1.
(Ⅱ)由题意知直AB的斜率存在.
AB:y=k(x-2),设A(x1,y1),B(x2,y2),P(x,y)
代入椭圆方程,得(1+2k2)x2-8k2x+8k2-2=0,
△=64k4-4(2k2+1)(8k2-2)>0,k2<
∴x1x2=
,x1+x2=
,
∵|
-
|<
,
∴
|x1-x2|<
,
∴(1+k2)[
-4×
]<
,
∴(4k2-1)(14k2+13)>0,
∴k2>
,
∴
<k2<
,
∵满足
+
=t
,
∴(x1+x2,y1+y2)=t(x,y),
∴x=
=
,y=
=
,
∵点P在椭圆上,
∴[
]2+2[
]2=2
∴16k2=t2(1+2k2)
∴t2=
=8-
,由于
<k2<
,
∴-2<t<-
或
<t<2
∴实数t取值范围为:-2<t<-
或
<t<2.
所以椭圆E的方程为:
| x2 |
| b2+1 |
| y2 |
| b2 |
解方程组
|
由于抛物线、椭圆都关于x轴对称,
∴
| |F2C| |
| |F2S| |
| |CD| |
| |ST| |
| 2 |
| ||
| 2 |
| ||
| 2 |
因此,
| 1 |
| b2+1 |
| 1 |
| 2b2 |
故椭圆的方程为
| x2 |
| 2 |
(Ⅱ)由题意知直AB的斜率存在.
AB:y=k(x-2),设A(x1,y1),B(x2,y2),P(x,y)
代入椭圆方程,得(1+2k2)x2-8k2x+8k2-2=0,
△=64k4-4(2k2+1)(8k2-2)>0,k2<
| 1 |
| 2 |
∴x1x2=
| 8k2-2 |
| 1+2k2 |
| 8k2 |
| 1+2k2 |
∵|
| PA |
| PB |
2
| ||
| 3 |
∴
| 1+k2 |
2
| ||
| 3 |
∴(1+k2)[
| (8k2)2 |
| (1+2k2)2 |
| 8k2-2 |
| 1+2k2 |
| 20 |
| 9 |
∴(4k2-1)(14k2+13)>0,
∴k2>
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
∵满足
| OA |
| OB |
| OP |
∴(x1+x2,y1+y2)=t(x,y),
∴x=
| x1+x2 |
| t |
| 8k2 |
| t(1+2k2) |
| y1+y2 |
| t |
| -4k |
| t(1+2k2) |
∵点P在椭圆上,
∴[
| 8k2 |
| t(1+2k2) |
| -4k |
| t(1+2k2) |
∴16k2=t2(1+2k2)
∴t2=
| 16k2 |
| 1+2k2 |
| 8 |
| 1+2k2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴-2<t<-
2
| ||
| 3 |
2
| ||
| 3 |
∴实数t取值范围为:-2<t<-
2
| ||
| 3 |
2
| ||
| 3 |

练习册系列答案
相关题目