题目内容
20.等差数列{an}的公差为2,且a1,a7,a37依次构成等比数列.(Ⅰ) 求数列{an}的通项公式及前n项和Sn;
(Ⅱ)数列{bn}满足bn=$\frac{1}{{S}_{n}}$,求数列{bn}的前n项和Tn.
分析 (Ⅰ)利用(a1+12)2=a1(a1+72)计算可知首项a1=3,进而可得结论;
(Ⅱ)通过裂项可知bn=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),并项相加即得结论.
解答 解:(Ⅰ)∵等差数列{an}的公差为2,
∴a7=a1+12,a37=a1+72,
又∵a1,a7,a37依次构成等比数列,
∴(a1+12)2=a1(a1+72),
解得a1=3,
∴数列{an}的通项an=3+2(n-1)=2n+1,
Sn=$\frac{n(3+2n+1)}{2}$=n(n+2);
(Ⅱ)∵Sn=n(n+2),
∴bn=$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
∴Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{1}{2(n+1)}$-$\frac{1}{2(n+2)}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知变量x与y正相关,且由观测数据算得样本平均数$\overline{x}$=3,$\overline{y}$=3.5,则由观测的数据得线性回归方程可能为( )
| A. | $\stackrel{∧}{y}$=-2x+9.5 | B. | $\stackrel{∧}{y}$=-0.3x+4.2 | C. | $\stackrel{∧}{y}$=0.4x+2.3 | D. | $\stackrel{∧}{y}$=2x-2.4 |
8.某学校为了解该校高三年级学生在市一练考试的数学成绩情况,随机从该校高三文科与理科各抽取50名学生的数学成绩,作出频率分布直方图如图,规定考试成绩[120,150]内为优秀.
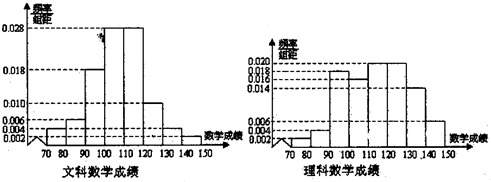
(1)由以上频率分布直方图填写下列2×2列联表,若按是否优秀来判断,是否有99%的把握认为该校的文理科数学成绩有差异.
(2)某高校派出2名教授对该校随机抽取的学生中一练数学成绩在140分以上的学生进行自主招生面试,每位教授至少面试一人,每位学生只能被一位教授面试,若甲教授面试的学生人数为ξ,求ξ的分布列和数学期望.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;

(1)由以上频率分布直方图填写下列2×2列联表,若按是否优秀来判断,是否有99%的把握认为该校的文理科数学成绩有差异.
| 文科 | 理科 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 | 50 | 50 | 100 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;
| P(K2>k) | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |
5.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2015年农村居民家庭人均纯收入.
附:回归直线y=bx+a的斜率和截距的最小二乘估计公式分别为:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,预测该地区2015年农村居民家庭人均纯收入.
附:回归直线y=bx+a的斜率和截距的最小二乘估计公式分别为:b=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,a=$\overline{y}$-b$\overline{t}$.
12. 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(表中w1=$\sqrt{x}$1,$\overline w$=$\frac{1}{8}$$\sum_{i=1}^n{w_i}$)
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(表中w1=$\sqrt{x}$1,$\overline w$=$\frac{1}{8}$$\sum_{i=1}^n{w_i}$)
(Ⅰ)根据散点图判断,y=a+bx与y=c+d$\sqrt{x}$,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);
(Ⅱ)根据( I)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据( II)的结果回答下列问题:
(i)当年宣传费x=90时,年销售量及年利润的预报值时多少?
(ii)当年宣传费x为何值时,年利润的预报值最大?
 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(表中w1=$\sqrt{x}$1,$\overline w$=$\frac{1}{8}$$\sum_{i=1}^n{w_i}$)
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.(表中w1=$\sqrt{x}$1,$\overline w$=$\frac{1}{8}$$\sum_{i=1}^n{w_i}$)| $\overline x$ | $\overline y$ | $\overline w$ | $\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}$ | $\sum_{i=1}^n{{{({w_i}-\overline w)}^2}}$ | $\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}$ | $\sum_{i=1}^n{({w_i}-\overline w)({y_i}-\overline y)}$ |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(Ⅱ)根据( I)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x,y的关系为z=0.2y-x,根据( II)的结果回答下列问题:
(i)当年宣传费x=90时,年销售量及年利润的预报值时多少?
(ii)当年宣传费x为何值时,年利润的预报值最大?