题目内容
8.某学校为了解该校高三年级学生在市一练考试的数学成绩情况,随机从该校高三文科与理科各抽取50名学生的数学成绩,作出频率分布直方图如图,规定考试成绩[120,150]内为优秀.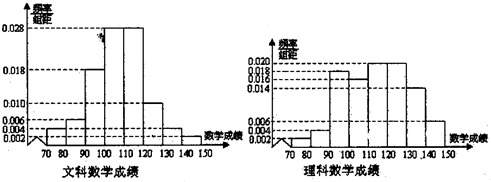
(1)由以上频率分布直方图填写下列2×2列联表,若按是否优秀来判断,是否有99%的把握认为该校的文理科数学成绩有差异.
| 文科 | 理科 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 | 50 | 50 | 100 |
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;
| P(K2>k) | 0.10 | 0.025 | 0.010 |
| K2 | 2.706 | 5.024 | 6.635 |
分析 (1)由频率分布直方图,确定表中数据,可得2×2列联表,计算K2,即可判断是否有99%的把握认为该校的文理科数学成绩有差异.
(2)确定变量的取值,求出相应的概率,即可求ξ的分布列和数学期望.
解答 解:(1)由频率分布直方图知,该校的文科数学成绩优秀的人数为(0.010+0.004+0.002)×10×50=8人,故非优秀人数为50-8=42人,该校的理科数学成绩优秀的人数为(0.020+0.014+0.006)×10×50=20人,故非优秀人数为50-20=30人
2×2列联表
| 文科 | 理科 | 总计 | |
| 优秀 | 8 | 20 | 28 |
| 非优秀 | 42 | 30 | 72 |
| 总计 | 50 | 50 | 100 |
所以有99%的把握认为该校的文理科数学成绩有差异.
(2)由(1)知,ξ=1,2,3.
P(ξ=1)=$\frac{{C}_{4}^{1}}{14}$=$\frac{2}{7}$,P(ξ=2)=$\frac{{C}_{4}^{2}{C}_{2}^{2}}{14}$=$\frac{3}{7}$,P(ξ=3)=$\frac{{C}_{4}^{3}}{14}$=$\frac{2}{7}$,
所以ξ的分布列为
| ξ | 1 | 2 | 3 |
| P | $\frac{2}{7}$ | $\frac{2}{7}$ |
点评 本题主要考查独立性检验的应用,考查离散型随机变量的分布列与期望,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于中档题.

练习册系列答案
相关题目
16.若a>b≥2,给定下列不等式①$\frac{1}{a}$<$\frac{1}{b}$;②a+b>2$\sqrt{ab}$;③ab>a+b;④loga3>logb3,其中正确的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
3.已知c<d,a>b>0,下列不等式中必成立的一个是( )
| A. | a+c>b+d | B. | a-c>b-d | C. | ad<bc | D. | $\frac{a}{c}$>$\frac{b}{d}$ |
17.数列{an}的前n项和Sn=2n(n∈N*),则a12+a22+…+an2等于( )
| A. | 4n | B. | $\frac{1}{3}({4^n}-1)$ | C. | $\frac{4}{3}({4^n}-1)$ | D. | $\frac{1}{3}({4^n}+8)$ |