题目内容
已知函数f(x)=sin(2x+ ).
).
(1)求函数y=f(x)的单调递减区间.
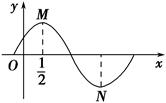
(2)画出函数y=f(x)在区间[0,π]上的图象.
 ).
).(1)求函数y=f(x)的单调递减区间.
(2)画出函数y=f(x)在区间[0,π]上的图象.
(1) [kπ+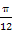 ,kπ+
,kπ+ ](k∈Z) (2)见解析
](k∈Z) (2)见解析
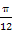 ,kπ+
,kπ+ ](k∈Z) (2)见解析
](k∈Z) (2)见解析(1)由2kπ+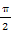 ≤2x+
≤2x+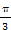 ≤2kπ+
≤2kπ+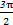 (k∈Z),
(k∈Z),
得kπ+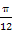 ≤x≤kπ+
≤x≤kπ+ (k∈Z).
(k∈Z).
∴函数的单调递减区间是[kπ+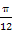 ,kπ+
,kπ+ ](k∈Z).
](k∈Z).
(2)∵0≤x≤π,∴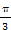 ≤2x+
≤2x+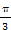 ≤
≤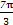 .列表如下:
.列表如下:
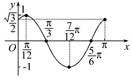
画出图象如图所示:
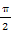 ≤2x+
≤2x+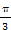 ≤2kπ+
≤2kπ+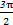 (k∈Z),
(k∈Z),得kπ+
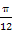 ≤x≤kπ+
≤x≤kπ+ (k∈Z).
(k∈Z).∴函数的单调递减区间是[kπ+
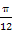 ,kπ+
,kπ+ ](k∈Z).
](k∈Z).(2)∵0≤x≤π,∴
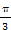 ≤2x+
≤2x+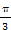 ≤
≤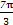 .列表如下:
.列表如下:| x | 0 | 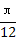 | 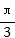 | 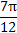 | 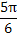 | π |
2x+ | 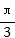 | 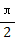 | π | 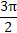 | 2π | 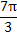 |
| y |  | 1 | 0 | -1 | 0 |  |


练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
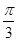 ,则f
,则f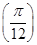 =__________.
=__________.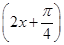 的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的
的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的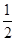 倍,所得图象关于直线x=
倍,所得图象关于直线x=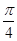 对称.则φ的最小正值为( )
对称.则φ的最小正值为( )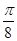
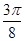
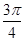
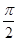
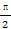 ,1).
,1).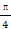 )=
)=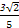 且α∈(0,
且α∈(0, sin2x-
sin2x- -
- .
. ,
, ],求函数f(x)的最值及对应的x的值.
],求函数f(x)的最值及对应的x的值.



 对称,则|φ|的最小值是( )
对称,则|φ|的最小值是( )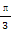


 cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为
cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为 ,则函数f(x)的单调递增区间为________.
,则函数f(x)的单调递增区间为________.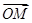 ·
·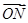 =0,则函数f(x)的最小正周期是________.
=0,则函数f(x)的最小正周期是________.