题目内容
18.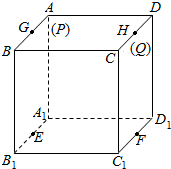 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )| A. | 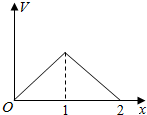 | B. | 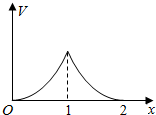 | ||
| C. | 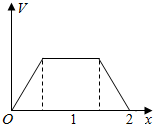 | D. | 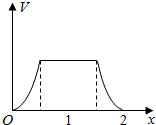 |
分析 运用上底面的中心O.确定面OEF,分割为等体积的三棱锥,它的底面积为定值,求解高即可
分类讨论得出当0$≤x≤\frac{1}{2}$时,VPEFQ═$\frac{x}{3}$,当$\frac{1}{2}<$x$≤\frac{3}{2}$时,VPEFQ=$\frac{1}{6}$=定值.当$\frac{3}{2}$<x≤2时,VPEFQ=$\frac{2}{3}$$-\frac{1}{3}$x,
判断即可得出函数图象.
解答 解:(1)当0$≤x≤\frac{1}{2}$时,点P与点Q运动的速度相等根据下图得出:面OEF把几何体PEFQ分割为相等的几何体,
∵S△OEF=$\frac{1}{2}×1×1$=$\frac{1}{2}$,P到面OEF的距离为x,
VPEFQ=2VP-OEF=2×$\frac{1}{3}×$$\frac{1}{2}$x=2•$\frac{x}{6}$=$\frac{x}{3}$,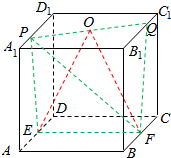 $\frac{2}{3}$
$\frac{2}{3}$
(2)当$\frac{1}{2}<$x$≤\frac{3}{2}$时,P在AB上,Q在C1D1上,P到$\frac{1}{2}$,S△OEF=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
VPEFQ=2VP-OEF=2×$\frac{1}{3}×\frac{1}{2}×\frac{1}{2}$=$\frac{1}{6}$=定值.
(3)当$\frac{3}{2}$<x≤2时,S△OEF=$\frac{1}{2}×1×1$=$\frac{1}{2}$,P到面OEF的距离为2-x,
VPEFQ=2VP-OEF=2×$\frac{1}{3}×\frac{1}{2}×$(2-x)=$\frac{2}{3}$$-\frac{1}{3}$x,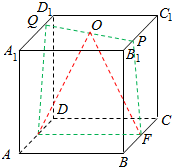
V=$\left\{\begin{array}{l}{\frac{x}{3},0≤x<\frac{1}{2}}\\{\frac{1}{6},\frac{1}{2}≤x<\frac{3}{2}}\\{\frac{2}{3}-\frac{1}{3}x,\frac{3}{2}≤x≤2}\end{array}\right.$
故选:C
点评 本题难度较大,考查了学生的空间能力,计算能力,运用几何图形分析问题的能力,分段函数的性质,图象,属于难题.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | $\frac{2}{e}$ | B. | 1 | C. | 2 | D. | e |
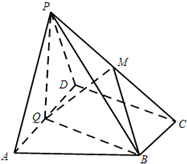 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.