题目内容
3.已知正数a,b,c满足a2+b2+c2=6.(Ⅰ)求a+2b+c的最大值M;
(Ⅱ)在(Ⅰ)的条件下,若不等式|x+1|+|x+m|≥M恒成立,求实数m的取值范围.
分析 (Ⅰ)分析题目已知a2+b2+c2=6,求a+2b+c的最大值,考虑到柯西不等式(a2+b2+c2)(12+22+12)≥(a+2b+c)2,即可得到答案.
(Ⅱ)利用绝对值不等式的几何意义可求得|x+1|+|x+m|≥|x+1-(x+m)|=|m-1|,由题意及(Ⅰ)得,|m-1|≥6,从而可求得实数m的取值范围.
解答 解:(Ⅰ)因为已知a、b、c是实数,且a2+b2+c2=6,
根据柯西不等式有(a2+b2+c2)(12+22+12)≥(a+2b+c)2
故(a+2b+c)2≤36,即a+2b+c≤6
即a+2b+c的最大值为6,
当且仅当$\frac{a}{1}=\frac{b}{2}=\frac{c}{1}$,即当a=c=1,b=2时取得最大值.…(4分)
(Ⅱ)因为|x+1|+|x+m|≥|x+1-(x+m)|=|m-1|,
由题意及(Ⅰ)得,|m-1|≥6,得m≥7或m≤-5.
综上,实数m的取值范围为m≥7或m≤-5.…(7分)
点评 本题考查柯西不等式,考查绝对值不等式的解法,掌握绝对值不等式的几何意义是解决问题的关键,属于中档题.

练习册系列答案
相关题目
13.甲乙两位同学最近五次模考数学成绩茎叶图如图,则平均分数较高和成绩比较稳定的分别是( )
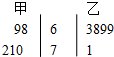
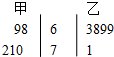
| A. | 甲、甲 | B. | 乙、甲 | C. | 甲、乙 | D. | 乙、乙 |
11.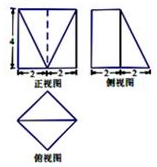 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )
 若一个几何体的三视图如图所示,则该几何体的体积是( )
若一个几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{160}{3}$ |
8.函数y=log${\;}_{\frac{1}{2}}$(sin2xcos$\frac{π}{4}$-cos2xsin$\frac{π}{4}$)的单调递减区间是( )
| A. | (kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$),k∈Z | B. | (kπ+$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | ||
| C. | (kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$),k∈Z | D. | (kπ+$\frac{3π}{8}$,kπ+$\frac{5π}{8}$),k∈Z |
13.P是△AOB所在平面上一点,且在AB的垂直平分线上,若|OA|=3,|OB|=2,则$\overrightarrow{OP}$•$\overrightarrow{AB}$=( )
| A. | $\frac{3}{2}$ | B. | -3 | C. | -$\frac{5}{2}$ | D. | 5 |
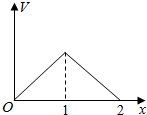
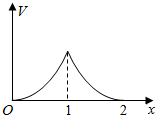
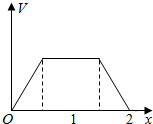
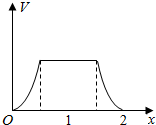
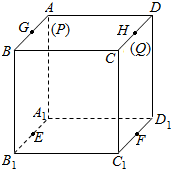 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )