题目内容
7.已知函数定义如下表| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 1 | 4 | 2 | 5 | 3 |
(1)求a6的值;
(2)求a1+a2+…+a2013的值.
分析 根据a0=5,an+1=f(an),n∈N和表格依次求出a1=4,a2=1、a3=5、a4=2、a5=4,判断出数列具有周期性,再由周期性求出a2013的值.
解答 解:(1)∵a0=5,an+1=f(an),n∈N,
∴a1=f(a0)=f(5)=3,
a2=f(a1)=f(3)=2,a3=f(a2)=f(2)=4,
a4=f(a3)=f(4)=5,a5=f(a4)=f(5)=3,
a6=f(a5)=f(3)=2,
(2)数列{an}各项是:3,2,4,5,3,2,4,5,3,…,
周期为4依次循环的数列,a1+a2+a3+a4=3+2+4+5=14,
a1+a2+…+a2013=14×503+a1=7045,
点评 本题考查数列的递推公式,以及数列周期性的应用,数列求和,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设i是虚数单位,则复数1-2i+3i2-4i3等于( )
| A. | -2-6i | B. | -2+2i | C. | 4+2i | D. | 4-6i |
17.若全集U={x∈R|x2≤4},A={x∈R|-2≤x≤0},则∁UA=( )
| A. | (0,2) | B. | [0,2) | C. | (0,2] | D. | [0,2] |
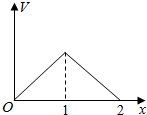
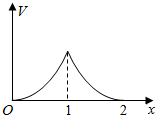
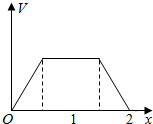
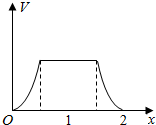
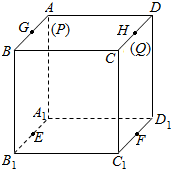 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )