题目内容
13.对于函数f(x)=log${\;}_{\frac{1}{2}}$(x2-ax+3),解答下列问题:(1)若f(x)的定义域是R,求a的取值范围;
(2)若f(x)的值域是R,求a的取值范围;
(3)若f(x)在[-1,+∞)内上有意义,求a的取值范围;
(4)若f(x)的值域是(-∞,-1],求a的取值范围;
(5)若f(x)在(-∞,-1]内为增函数,求a的取值范围.
分析 (1)转化为x2-ax+3>0在R上恒成立,利用二次函数性质求解即可.
(2)判断得出y=x2-ax+3的图象不能在x轴上方,即△=a2-12≥0求解.
(3)转化x2-ax+3>0在[-1,+∞)上恒成立,根据二次函数性质得出△<0或$\left\{\begin{array}{l}{\frac{a}{2}≤-′1}\\{4+a>0}\end{array}\right.$.
(4)利用复合函数性质得出:y=x2-ax+3的值域为[2,+∞),最小值$\frac{4×1×3-{a}^{2}}{4}$=2,求解即可.
(5)根据复合函数的单调性得出y=x2-ax+3在(-∞,-1]内为减函数,且x2-ax+3>0在(-∞,-1]恒成立.再利用二次函数性质求解即可.
解答 解:对于函数f(x)=log${\;}_{\frac{1}{2}}$(x2-ax+3),
(1)∵f(x)的定义域是R,
∴x2-ax+3>0在R上恒成立,
即△=a2-12<0,
得:a∈(-2$\sqrt{3}$,2$\sqrt{3}$)
(2)∵f(x)的值域是R,
∴y=x2-ax+3的图象不能在x轴上方,
即△=a2-12≥0,得:a∈(-∞,-2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞)
(3)∵f(x)在[-1,+∞)内上有意义,
∴x2-ax+3>0在[-1,+∞)上恒成立,
即△<0或$\left\{\begin{array}{l}{\frac{a}{2}≤-′1}\\{4+a>0}\end{array}\right.$
得a∈(-2$\sqrt{3}$,2$\sqrt{3}$)∪(-4,-2),
(4)∵f(x)的值域是(-∞,-1],
∴y=x2-ax+3的值域为[2,+∞),
$\frac{4×1×3-{a}^{2}}{4}$=2,即a=±2,
故a的取值范围:a=-2或a=2
(5)∵f(x)在(-∞,-1]内为增函数,
∴y=x2-ax+3在(-∞,-1]内为减函数,且x2-ax+3>0在(-∞,-1]恒成立.
∴$\left\{\begin{array}{l}{\frac{a}{2}≥-1}\\{(-1)^{2}-a(-1)+3>0}\end{array}\right.$即a≥-2.
点评 本题结合对数函数的单调性,复合函数的单调性的应用与二次函数及对数函数的性质,还考查了二次函数在区间上单调,但不要忽略了函数的定义域,

| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
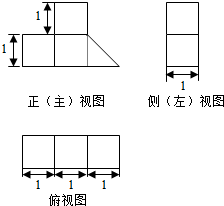
| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
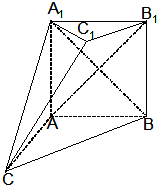 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,△A1CB是等边三角形,AC=AB=1,B1C1∥BC,BC=2B1C1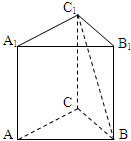 如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.
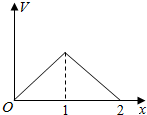
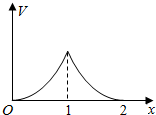
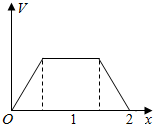
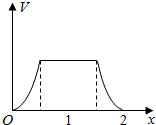
如图,在三棱柱ABC-A1B1C1中,底面是边长为1的正三角形,AA1⊥平面ABC,AA1=$\sqrt{2}$,则BC1与侧面ACC1A1所成的角的大小为$\frac{π}{6}$.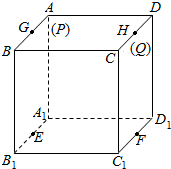 在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )
在边长为1的正方体中,E,F,G,H分别为A1B1,C1D1,AB,CD的中点,点P从G出发,沿折线GBCH匀速运动,点Q从H出发,沿折线HDAG匀速运动,且点P与点Q运动的速度相等,记E,F,P,Q四点为顶点的三棱锥的体积为V,点P运动的路程为x,在0≤x≤2时,V与x的图象应为( )