题目内容
9.变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$,若Z=2x-y的最大值为2,则实数m等于1.分析 作出可行域,变形目标函数可得y=2x-Z,平移直线经过点A时,目标函数取最大值2,解出A的坐标可得m的方程,解方程可得m值.
解答 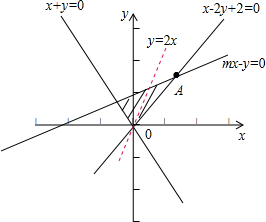 解:作出约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$所对应的可行域(如图阴影),
解:作出约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$所对应的可行域(如图阴影),
变形目标函数可得y=2x-Z,平移直线经过点A时,目标函数取最大值2,
联立$\left\{\begin{array}{l}{x-2y+2=0}\\{mx-y=0}\end{array}\right.$可解得$\left\{\begin{array}{l}{x=\frac{2}{2m-1}}\\{y=\frac{2m}{2m-1}}\end{array}\right.$,即点A($\frac{2}{2m-1}$,$\frac{2m}{2m-1}$),
∴2×$\frac{2}{2m-1}$-$\frac{2m}{2m-1}$=2,解得m=1
故答案为:1
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知函数f(x)=sinx,f(x)的导数是( )
| A. | 偶函数 | B. | 奇函数 | C. | 增函数 | D. | 减函数 |
20.样本中共有五个个体,其值分别为-1,0,2,3,a,若该样本的平均值为1,则样本方差为( )
| A. | $\sqrt{\frac{6}{5}}$ | B. | $\frac{6}{5}$ | C. | $\sqrt{2}$ | D. | 2 |
17.若z(1+i)=i(其中i为虚数单位),则|z|等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
14.设函数f′(x)的偶函数f(x)(x∈R且x≠0)的导函数,f(2)=0且当x>0时,xf′(x)-f(x)>0,则使f(x)<0成立的x的取值范围为( )
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-∞,-2)∪(2,+∞) |
1.已知随机变量X~N(3,1),且P(2≤X≤4)=0.6626,则P(X>4)=( )
| A. | 0.1685 | B. | 0.1686 | C. | 0.1687 | D. | 0.1688 |
19.(A)设函数f(x)=xcosx-sinx,x∈(0,π),则f(x)的单调性是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减函数 | D. | 先减后增函数 |
 已知函数f(x)=sin(2x-$\frac{π}{6}$)
已知函数f(x)=sin(2x-$\frac{π}{6}$)