题目内容
14.设函数f′(x)的偶函数f(x)(x∈R且x≠0)的导函数,f(2)=0且当x>0时,xf′(x)-f(x)>0,则使f(x)<0成立的x的取值范围为( )| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-∞,-2)∪(2,+∞) |
分析 构造函数g(x)=$\frac{f(x)}{x}$,利用导数得到,g(x)在(0,+∞)是增函数,再根据f(x)为奇函数,根据f(2)=0,解得f(x)<0的解集.
解答 解:令g(x)=$\frac{f(x)}{x}$,
∴g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵x>0时,xf′(x)-f(x)>0,
∴x>0时,g′(x)>0,
∴g(x)在(0,+∞)上是增函数,
∵f(2)=0,
∴g(2)=$\frac{f(2)}{2}$=0,
当0<x<2,
g(x)<g(2)=0,即f(x)<0,
当x>2时,g(x)>g(2)=0,即f(x)>0,
∵f(x)是偶函数,
∴当-2<x<0,f(x)<0,
故不等式f(x)<0的解集是(-2,0)∪(0,2),
故选:B.
点评 本题考查了抽象函数的奇偶性与单调性,考查了构造函数及数形结合的思想.解决本题的关键是能够想到通过构造函数解决.

练习册系列答案
相关题目
4.复数z1,z2互为共轭复数,若z1=1-2i,则z1-z2=( )
| A. | -4i | B. | 4i | C. | 0 | D. | 2 |
2.已知α的终边在第一象限,则角$\frac{α}{2}$的终边在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第一或第三象限 | D. | 第一或第四象限 |
3.命题p:?x∈R,2x<3x;命题q:?x∈R,$\sqrt{x}=lo{g}_{\frac{1}{2}}x$,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
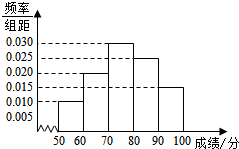 对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )
对某次联考数学成绩(百分制)进行分析,如图为分析结果的频率分布直方图.根据标准,成绩分数在区间[50,60)上为不及格,在[60,70)上为一般,在[70,80)上为较好,在[80,90)上为良好,在[90,100]上为优秀.用频率估计概率,若从参考学生中随机抽取1人,则其成绩为优良(优秀或良好)的概率为( )