题目内容
过抛物线焦点F的直线与抛物线交于A、B两点,若A、B在抛物线准线上的射影为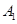 、
、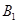 ,则∠
,则∠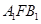 =
=
A.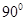 B.
B. 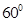 C.
C. 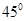 D.
D. 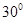
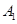 、
、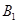 ,则∠
,则∠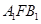 =
=A.
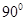 B.
B. 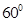 C.
C. 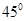 D.
D. 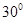
A
分析:由抛物线的定义及内错角相等,可得∠AFA1=∠A1FK,同理可证∠BFB1=∠B1FK,由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,可得答案.
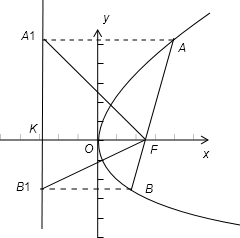
解:如图:设准线与x轴的交点为K,∵A、B在抛物线的准线上的射影为A1、B1,
由抛物线的定义可得,AA1=AF,∴∠AA1F=∠AFA1,又由内错角相等得∠AA1F=∠A1FK,∴∠AFA1=∠A1FK.
同理可证∠BFB1=∠B1 FK. 由∠AFA1+∠A1FK+∠BFB1+∠B1FK=180°,
∴∠A1FK+∠B1FK=∠A1FB1=90°,
故选A。

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
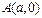 和
和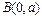 的直线与抛物线
的直线与抛物线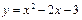 没有交点,那么实数
没有交点,那么实数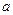 的取值范围是
的取值范围是 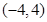 的抛物线的标准方程是( )
的抛物线的标准方程是( )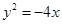
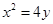
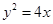 或
或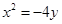
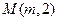 到焦点F的距离为
到焦点F的距离为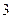 .
.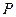 的方程;
的方程;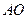 ,
,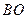 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.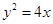 的焦点是
的焦点是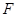 ,准线是
,准线是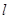 ,则经过点
,则经过点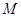 (4,4)且与
(4,4)且与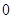 个
个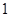 个
个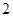 个
个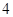 个
个 知抛物线
知抛物线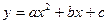 通过点P(1,1),且在点Q(2,-1)处与直线
通过点P(1,1),且在点Q(2,-1)处与直线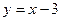 相切,求实数
相切,求实数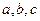 的值.
的值. 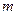 时,水面宽4
时,水面宽4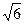
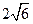
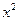 上的动点,点M到直线2x-y-a=0(a为常数)的最短距离为
上的动点,点M到直线2x-y-a=0(a为常数)的最短距离为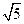 ,则实数a的值为
,则实数a的值为