题目内容
若抛物线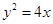 的焦点是
的焦点是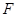 ,准线是
,准线是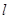 ,则经过点
,则经过点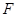 、
、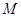 (4,4)且与
(4,4)且与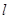 相切的圆共有
相切的圆共有
第Ⅱ卷
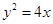 的焦点是
的焦点是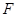 ,准线是
,准线是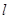 ,则经过点
,则经过点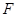 、
、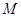 (4,4)且与
(4,4)且与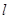 相切的圆共有
相切的圆共有 A.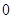 个 个 | B.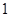 个 个 | C.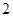 个 个 | D.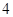 个 个 |
C
分析:根据抛物线的方程求得焦点坐标和准线的方程,设出所求圆的圆心,表示出半径,则圆的方程可得,把M,F点的坐标代入整理求得h,和g,则圆的方程可得.
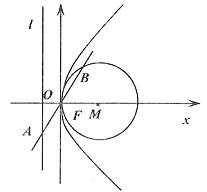
解:抛物线y2=4x的焦参数p=2,所以F(1,0),直线l:x=-1,即x+1=0,
设经过点M(4,4)、F(1,0),且与直线l相切的圆的圆心为Q(g,h),
则半径为Q到,l的距离,即1+g,所以圆的方程为(x-g)2+(y-h)2=(1+g)2,
将M、F的坐标代入,得(4-g)2+(4-h)2=(1+g)2,(1-g)2+(0-h)2=(1+g)2,
即h2-8h+1=10g①,
h2=4g②,②代入①,
得3h2+16h-2=0,
解得h1=
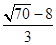 ,h2=-
,h2=-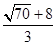 ,(经检验无增根)
,(经检验无增根)代入②得g1=
 ,g2=
,g2=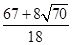 ,
,所以满足条件的圆有两个:
(x-
 )2+(y-
)2+(y-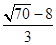 )2=(
)2=(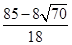 )2,
)2,(x-
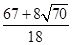 )2+(y+
)2+(y+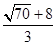 )2=(
)2=( )2.
)2.故选C

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
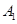 、
、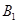 ,则∠
,则∠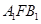 =
=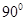 B.
B. 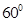 C.
C. 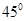 D.
D. 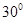
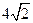 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?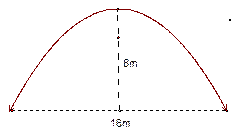
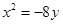 的准线方程为
的准线方程为 2
2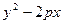 (p为常数)的准线与X轴交于点K,过K的直线l与抛物线交于A、B两点,则
(p为常数)的准线与X轴交于点K,过K的直线l与抛物线交于A、B两点,则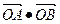 = 。
= 。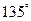 的直线,被抛物线所截得的弦长为8,试求抛物线的标准方程.
的直线,被抛物线所截得的弦长为8,试求抛物线的标准方程.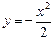 与过点
与过点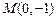 的直线
的直线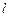 相交于
相交于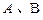 两点,
两点,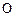 为原点.若
为原点.若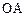 和
和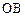 的斜率之和为1,(1)求直线
的斜率之和为1,(1)求直线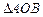 的面积.
的面积.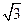 x-y-
x-y-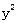 =4x相交于A、B两点,与x轴相交于点F,
=4x相交于A、B两点,与x轴相交于点F,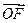 =λ
=λ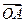 +μ
+μ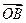 (λ≤μ),则
(λ≤μ),则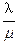 =_______.
=_______.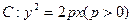 的准线为
的准线为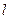 ,焦点为F,
,焦点为F,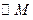 的圆心在
的圆心在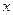 轴的正半轴上,且与
轴的正半轴上,且与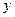 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为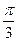 的直线
的直线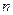 ,交
,交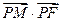 的最小值;
的最小值;