题目内容
(本小题共14分)
已知抛物线P:x2="2py" (p>0).
(Ⅰ)若抛物线上点
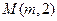 到焦点F的距离为
到焦点F的距离为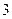 .
.(ⅰ)求抛物线
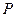 的方程;
的方程;(ⅱ)设抛物线
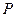 的准线与y轴的交点为E,过E作抛物线
的准线与y轴的交点为E,过E作抛物线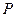 的切线,求此切线方程;
的切线,求此切线方程;(Ⅱ)设过焦点F的动直线l交抛物线于A,B两点,连接
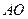 ,
,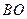 并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.
并延长分别交抛物线的准线于C,D两点,求证:以CD为直径的圆过焦点F.解:(Ⅰ)(ⅰ)由抛物线定义可知,抛物线上点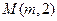 到焦点F的距离与到准线距离相等,
到焦点F的距离与到准线距离相等,
即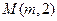 到
到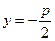 的距离为3;
的距离为3;
∴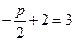 ,解得
,解得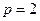 .
.
∴ 抛物线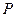 的方程为
的方程为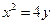 . ………………4分
. ………………4分
(ⅱ)抛物线焦点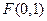 ,抛物线准线与y轴交点为
,抛物线准线与y轴交点为 ,
,
显然过点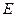 的抛物线的切线斜率存在,设为
的抛物线的切线斜率存在,设为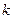 ,切线方程为
,切线方程为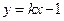 .
.
由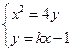 , 消y得
, 消y得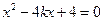 , ………………6分
, ………………6分
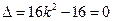 ,解得
,解得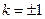 . ………………7分
. ………………7分
∴切线方程为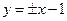 . ………………8分
. ………………8分
(Ⅱ)直线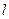 的斜率显然存在,设
的斜率显然存在,设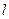 :
: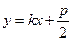 ,
,
设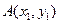 ,
,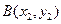 ,
,
由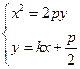 消y得
消y得 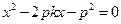 . 且
. 且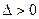 .
.
∴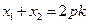 ,
,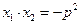 ;
;
∵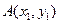 , ∴ 直线
, ∴ 直线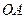 :
: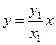 ,
,
与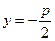 联立可得
联立可得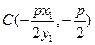 , 同理得
, 同理得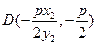 .……………10分
.……………10分
∵ 焦点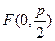 ,
,
∴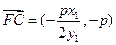 ,
,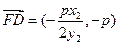 , ………………12分
, ………………12分
∴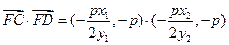
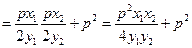
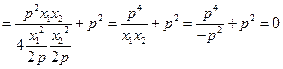
∴ 以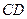 为直径的圆过焦点
为直径的圆过焦点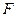 . ………………14分
. ………………14分
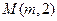 到焦点F的距离与到准线距离相等,
到焦点F的距离与到准线距离相等,即
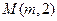 到
到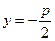 的距离为3;
的距离为3;∴
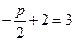 ,解得
,解得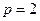 .
.∴ 抛物线
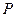 的方程为
的方程为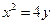 . ………………4分
. ………………4分(ⅱ)抛物线焦点
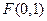 ,抛物线准线与y轴交点为
,抛物线准线与y轴交点为 ,
,显然过点
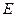 的抛物线的切线斜率存在,设为
的抛物线的切线斜率存在,设为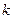 ,切线方程为
,切线方程为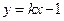 .
.由
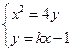 , 消y得
, 消y得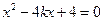 , ………………6分
, ………………6分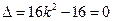 ,解得
,解得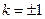 . ………………7分
. ………………7分∴切线方程为
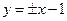 . ………………8分
. ………………8分(Ⅱ)直线
 的斜率显然存在,设
的斜率显然存在,设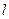 :
: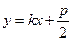 ,
,设
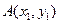 ,
,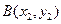 ,
,由
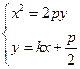 消y得
消y得 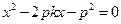 . 且
. 且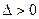 .
.∴
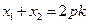 ,
,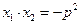 ;
;∵
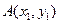 , ∴ 直线
, ∴ 直线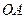 :
: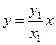 ,
, 与
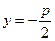 联立可得
联立可得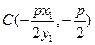 , 同理得
, 同理得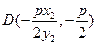 .……………10分
.……………10分∵ 焦点
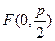 ,
,∴
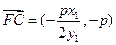 ,
,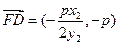 , ………………12分
, ………………12分∴
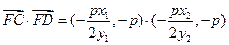
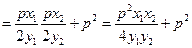
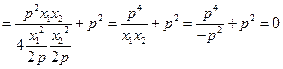
∴ 以
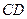 为直径的圆过焦点
为直径的圆过焦点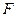 . ………………14分
. ………………14分略

练习册系列答案
相关题目
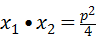 是P1P2过抛物线焦点的( )
是P1P2过抛物线焦点的( )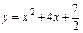 ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M的法线的斜率为
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.若C在点M的法线的斜率为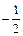 ,求点M的坐标(x0,y0)
,求点M的坐标(x0,y0)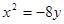 的准线方程是( ).
的准线方程是( ).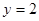
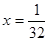

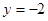
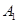 、
、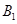 ,则∠
,则∠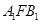 =
=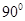 B.
B. 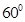 C.
C.  D.
D. 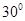
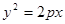 的焦点与椭圆
的焦点与椭圆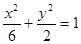 的右焦点重合,则
的右焦点重合,则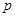 的值为 ( )
的值为 ( )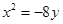 的准线方程为
的准线方程为 2
2 ,过点
,过点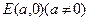 的直线交抛物线于点
的直线交抛物线于点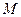 、
、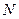 ,
, ,若
,若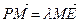 ,
, ,则
,则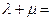 ( )
( )