Question

12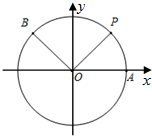．如图，A是单位圆与x轴正半轴的交点，点P、B在单位圆上，设∠AOP=θ，∠AOB=α，且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$．
（Ⅰ）记四边形OAQP的面积为S，当0＜θ＜π时，$\overrightarrow{OA}$.$\overrightarrow{OQ}$+S求的最大值及此时θ的值；
（Ⅱ）若α≠$\frac{kπ}{2}$，θ≠kπ（k∈Z），且$\overrightarrow{OB}$∥$\overrightarrow{OQ}$，求证：tanα=tan$\frac{θ}{2}$．

Answer 1

分析 （Ⅰ）根据三角函数的定义表示出点的坐标，利用向量数量积的公式将$\overrightarrow{OA}$.$\overrightarrow{OQ}$+S转化为三角函数形式，即可求的最大值及此时θ的值；
（Ⅱ）根据向量平行建立坐标关系，利用三角函数的关系式进行证明．

解答 解：（Ⅰ）由已知A（1，0），P（cosθ，sinθ）
∵$\overrightarrow{OQ}=\overrightarrow{OA}+\overrightarrow{OP}$，∴$\overrightarrow{OQ}=（1+cosθ，sinθ）$…（3分）
又S=sinθ，
∴$\overrightarrow{OA}•\overrightarrow{OQ}+S=sinθ+cosθ+1=\sqrt{2}sin（θ+\frac{π}{4}）+1$（0＜θ＜π）
故$\overrightarrow{OA}•\overrightarrow{OQ}+S$的最大值是$θ=\frac{π}{4}$，此时$θ=\frac{π}{4}$…（6分）
（Ⅱ）∵$\overrightarrow{OA}+\overrightarrow{OP}=（1+cosθ，sinθ）$，$\overrightarrow{OB}$∥$（{\overrightarrow{OA}+\overrightarrow{OP}}）$，
∴cosαsinθ-（1+cosθ）sinα=0…（9分）
又$α≠\frac{kπ}{2}$，θ≠kπ（k∈Z），
∴$tanα=\frac{sinθ}{1+cosθ}$=$\frac{{2sin\frac{θ}{2}cos\frac{θ}{2}}}{{2{{cos}^{_2}}\frac{θ}{2}}}=tan\frac{θ}{2}$…（12分）

点评 本题主要考查三角函数的化简和求值，根据向量数量积的坐标公式进行化简是解决本题的关键．