题目内容
1.计算:${∫}_{2}^{3}$($\sqrt{x}$+$\frac{1}{\sqrt{x}}$)2dx.分析 ${∫}_{2}^{3}$($\sqrt{x}$+$\frac{1}{\sqrt{x}}$)2dx化简为${∫}_{2}^{3}$(x+$\frac{1}{x}$+2)dx,再根据定积分的计算法则计算即可.
解答 解:${∫}_{2}^{3}$($\sqrt{x}$+$\frac{1}{\sqrt{x}}$)2dx=${∫}_{2}^{3}$(x+$\frac{1}{x}$+2)dx=($\frac{1}{2}{x}^{2}$+lnx+2x)|${\;}_{2}^{3}$=($\frac{9}{2}$+ln3+6)-(2+ln2+4)=$\frac{9}{2}$-ln$\frac{3}{2}$.
点评 本题考查了定积分的计算,关键是求出原函数,属于基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
6.过曲线y=x3+bx+c上一点A(1,2)的切线方程为y=x+1,则bc的值为( )
| A. | -6 | B. | 6 | C. | -4 | D. | 4 |
13.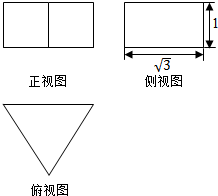 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )| A. | $\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 6+$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
10.甲、乙、丙三人独立地去译一个密码,分别译出的概率为$\frac{1}{5}$,$\frac{1}{3}$,$\frac{1}{4}$,则此密码能译出的概率是( )
| A. | $\frac{1}{60}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{59}{60}$ |
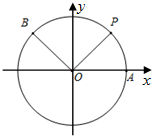 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.