题目内容
3.若数列{an}满足a1a2a3…an=n2+3n+2,在数列{an}的通项公式为an=$\left\{\begin{array}{l}{6,n=1}\\{\frac{n+2}{n},n≥2}\end{array}\right.$.分析 a1a2a3…an=n2+3n+2,当n≥2时,a1a2a3…an-1=n2+n,即可得出.
解答 解:∵a1a2a3…an=n2+3n+2,
∴当n≥2时,a1a2a3…an-1=(n-1)2+3(n-1)+2=n2+n,
∴an=$\frac{{n}^{2}+3n+2}{{n}^{2}+n}$=$\frac{n+2}{n}$.
当n=1时,a1=6.
∴an=$\left\{\begin{array}{l}{6,n=1}\\{\frac{n+2}{n},n≥2}\end{array}\right.$.
故答案为:an=$\left\{\begin{array}{l}{6,n=1}\\{\frac{n+2}{n},n≥2}\end{array}\right.$.
点评 本题查克拉递推式的应用、数列的通项公式,属于基础题.

练习册系列答案
相关题目
13.${∫}_{0}^{1}$(ex+2x)dx=( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
8.已知锐角α,β满足sinα=$\frac{2\sqrt{5}}{5}$,cosβ=$\frac{\sqrt{10}}{10}$,则α+β=( )
| A. | $\frac{π}{4}$ | B. | $\frac{3}{4}$π | C. | $\frac{π}{4}$或$\frac{3}{4}$π | D. | $\frac{π}{2}$ |
13.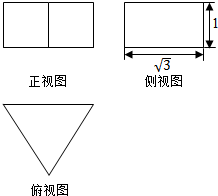 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )| A. | $\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 6+$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
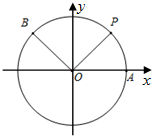 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.