题目内容
20.设{an}为等差数列,Sn为数列{an}的前n项和,已知a2+a5=1,S15=75,Tn为数列{Snn}的前n项和(n∈N*).(1)求Sn;
(2)求Tn,及Tn的最小值.
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出;
(2)由于Snn=n−52,利用等差数列的通项公式及其前n项和公式可得Tn,再利用二次函数的单调性即可得出.
解答 解:(1)∵{an}为等差数列,首项为a1,公差设为d,
则依题意有{(a1+d)+(a1+4d)=115a1+15×142d=75,
解得{a1=−2d=1,
∴Sn=a1n+n(n−1)2d=−2n+n(n−1)2=n2−5n2.
(2)∵Sn=n2−5n2,∴Snn=n−52.
设bn=Snn=n−52,则bn+1−bn=(n+1)−52−n−52=12,
∴数列{bn}是公差为12的等差数列,首项为b1=S11=a1=−2,
Tn为数列{Snn}的前n项和,
∴Tn=−2n+n(n−1)2•12=n2−9n4.
又∵y=x2−9x4图象开口向上,对称轴为x=92,且n∈N*,
∴n=4或n=5时,(Tn)min=42−9×44=−5.
点评 本题考查了等差数列的通项公式及其前n项和公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.汽车年检必须对尾气的碳排放量进行环保检测,二氧化碳排放量超过130g/km的轻型汽车被认为是超标.检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km).
经测算乙品牌轻型汽车二氧化碳排放量的平均值为¯x乙=120g/km.
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,求至少有一辆二氧化碳排放量超标的概率多少?
(2)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,求至少有一辆二氧化碳排放量超标的概率多少?
(2)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
8.已知锐角α,β满足sinα=2√55,cosβ=√1010,则α+β=( )
| A. | π4 | B. | 34π | C. | π4或34π | D. | π2 |
10.甲、乙、丙三人独立地去译一个密码,分别译出的概率为15,13,14,则此密码能译出的概率是( )
| A. | 160 | B. | 25 | C. | 35 | D. | 5960 |
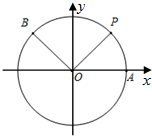 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且