题目内容
4.已知f(x)=4x3-12x2+a在[-2,2]上的最大值为3,求f(x)的最小值.分析 先求出函数f(x)的导数,取得函数的单调区间,从而求出a的值,进而求出函数的最小值.
解答 解:f′(x)=12x(x-2),
令f′(x)>0,解得:x<0,令f′(x)<0,解得:0<x<2,
∴f(x)在[-2,0)递增,在(0,2]递减,
∴f(x)最大值=f(0)=a=3,
∴f(x)=4x3-12x2+3,
而f(-2)=-77,f(2)=-13,
∴f(x)最小值=-13.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
13.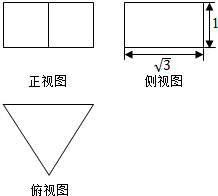 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )| A. | $\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 6+$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
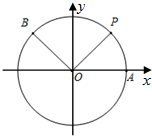 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.