题目内容
7．已知集合M={x|x2-4x＜0}，N={x|m＜x＜5}，若M∩N={x|3＜x＜n}，则m+n等于（ ）| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
分析 求出集合的等价条件，根据集合的基本运算进行求解即可．
解答 解：M={x|x2-4x＜0}={x|0＜x＜4}，
∵N={x|m＜x＜5}，
∴若M∩N={x|3＜x＜n}，
则m=3，n=4，
故m+n=3+4=7，
故选：C
点评 本题主要考查集合的基本运算，比较基础．
练习册系列答案
特高级教师点拨系列答案
相关题目
17．已知f（x）=$\frac{x}{{e}^{x}}$，定义f1（x）=f′（x），f2（x）=[f1（x）]′，…，fn+1（x）=[fn（x）]′，n∈N．经计算f1（x）=$\frac{1-x}{{e}^{x}}$，f2（x）=$\frac{x-2}{{e}^{x}}$，f3（x）=$\frac{3-x}{{e}^{x}}$，…，照此规律，则f2015（0）=（ ）
| A． | -2015 | B． | 2015 | C． | $\frac{2014}{e}$ | D． | -$\frac{2014}{e}$ |
如图所示，一圆柱内挖去一个圆锥，圆锥的顶点是圆柱底面的圆心，圆锥的底面是圆柱的另一个底面．圆柱的母线长为6，底面半径为2，求该几何体的表面积．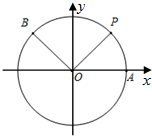
如图，A是单位圆与x轴正半轴的交点，点P、B在单位圆上，设∠AOP=θ，∠AOB=α，且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$．