题目内容
2.函数y=sin(cosx)的单调递减区间为[2kπ,2kπ+π],k∈Z.分析 利用换元法设t=cosx,则y=sint,根据复合函数单调性之间的关系进行求解即可.
解答 解:设t=cosx,则y=sint
∵-1≤cosx≤1,
∴-1≤t≤1,
则函数y=sint在[-1,1]上为增函数,
由复合函数单调性可知要求y=sin(cosx)的单调递减区间,
即求t=cosx的递减区间,
∵t=cosx的递减区间为[2kπ,2kπ+π],k∈Z,
∴函数y=sin(cosx)的单调递减区间为[2kπ,2kπ+π],k∈Z.
故答案为:[2kπ,2kπ+π],k∈Z.
点评 本题主要考查三角函数单调区间的求解,利用换元法结合复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
12.若α为第一象限角,则$\frac{α}{2}$为( )
| A. | 第一象限的角 | B. | 第一或第四象限的角 | ||
| C. | 第一或第三象限的角 | D. | 第二或第四象限的角 |
13.${∫}_{0}^{1}$(ex+2x)dx=( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
10.汽车年检必须对尾气的碳排放量进行环保检测,二氧化碳排放量超过130g/km的轻型汽车被认为是超标.检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km).
经测算乙品牌轻型汽车二氧化碳排放量的平均值为$\overline{{x}_{乙}}$=120g/km.
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,求至少有一辆二氧化碳排放量超标的概率多少?
(2)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
(1)从被检测的5辆甲品牌轻型汽车中任取2辆,求至少有一辆二氧化碳排放量超标的概率多少?
(2)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
17.已知f(x)=$\frac{x}{{e}^{x}}$,定义f1(x)=f′(x),f2(x)=[f1(x)]′,…,fn+1(x)=[fn(x)]′,n∈N.经计算f1(x)=$\frac{1-x}{{e}^{x}}$,f2(x)=$\frac{x-2}{{e}^{x}}$,f3(x)=$\frac{3-x}{{e}^{x}}$,…,照此规律,则f2015(0)=( )
| A. | -2015 | B. | 2015 | C. | $\frac{2014}{e}$ | D. | -$\frac{2014}{e}$ |
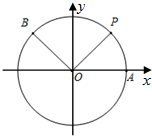 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.