题目内容
2.在△ABC中,内角A,B,C的对边分别为a,b,c,已知c=a(sinB+cosB).(1)求角A的大小;
(2)若边a=$\sqrt{2}$,求$\sqrt{2}$b-c的取值范围.
分析 (1)根据正弦定理、诱导公式和两角和与差的公式求得角A的大小;
(2)利用正弦定理求出b,c,利用两角和差的余弦公式进行化简即可得到结论.
解答 解:(1)∵在△ABC中,内角A,B,C的对边分别为a,b,c,c=a(sinB+cosB),
∴$\frac{a}{sinA}$=$\frac{a(sinB+cosB)}{sinC}$=$\frac{a(sinB+cosB)}{sin(A+B)}$,
∴sinAcosB+sinBcosA=sinAsinB+sinAcosB,即cosA=sinA,
∴A=45°;
(2)∵a=$\sqrt{2}$,A=45°,
∴$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=\frac{\sqrt{2}}{\frac{\sqrt{2}}{2}}$=2,
即b=2sinB,c=2sinC,且B+C=135°,B=135°-C,(0°<C<135°)
则$\sqrt{2}$b-c=2$\sqrt{2}$sinB-2sinC=2$\sqrt{2}$sin(135°-C)-2sinC
=2$\sqrt{2}$(-$\frac{\sqrt{2}}{2}$cosC+$\frac{\sqrt{2}}{2}$sinC)-2sinC
=-2cosC+2sinC-2sinC
=-2cosC,
∵0°<C<135°,
∴-$\frac{\sqrt{2}}{2}$<cosC<1,∴-$\sqrt{2}$<2cosC<2,
∴-2<-2cosC<$\sqrt{2}$,
故$\sqrt{2}$b-c的取值范围是(-2,$\sqrt{2}$).
点评 本题主要考查解三角形的应用,根据正弦定理以及两角和差的正弦公式是解决本题的关键.综合考查学生的运算能力.

 名校课堂系列答案
名校课堂系列答案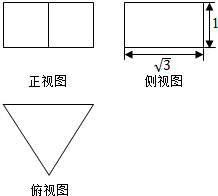 若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )
若正三棱柱(底面为正三角形,且侧棱与底面垂直的三棱柱)的三视图如图所示,该三棱柱的表面积是( )| A. | $\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 6+$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
| A. | $\frac{1}{60}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{59}{60}$ |
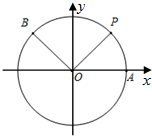 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.