题目内容
若抛物线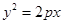 的焦点与椭圆
的焦点与椭圆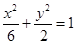 的右焦点重合,则
的右焦点重合,则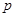 的值为 .
的值为 .
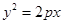 的焦点与椭圆
的焦点与椭圆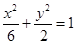 的右焦点重合,则
的右焦点重合,则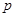 的值为 .
的值为 .4
分析:先根据椭圆方程求出椭圆的右交点坐标,因为抛物线y2=2px的焦点与椭圆x2/6+ y2/2=1的右焦点重合,所以抛物线的焦点坐标可知,再根据抛物线中焦点坐标为(p/2,0),即可求出p值。
解答:
∵x2/6+ y2/2=1 中a2=6,b2=2,∴c2=4,c=2
∴右焦点坐标为(2,0)
∵抛物线y2=2px的焦点与椭圆x2/6+ y2/2=1 的右焦点重合,
∴抛物线y2=2px中p=4
故答案为4。
点评:本题主要考查了椭圆焦点与抛物线焦点的求法,属于圆锥曲线的基础题。

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
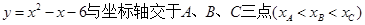 ,圆
,圆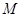 为
为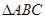 的外接圆,斜率为1的直线
的外接圆,斜率为1的直线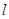 与圆
与圆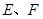 ,
,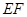 的中点为
的中点为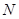 ,
,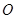 为坐标原点,且
为坐标原点,且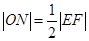 .
.
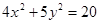 的焦点坐标( )
的焦点坐标( )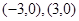
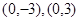

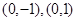
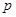 :对任意实数
:对任意实数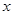 ,不等式
,不等式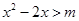 恒成立;命题
恒成立;命题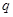 :方程
:方程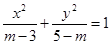 表示焦点在
表示焦点在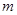 的取值范围;
的取值范围;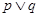 ”为真命题,且“
”为真命题,且“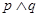 ”为假命题,求实数
”为假命题,求实数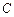 :
: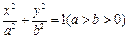 的离心率为
的离心率为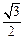 ,且过
,且过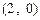 点.⑴求椭圆
点.⑴求椭圆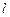 :
: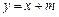 与椭圆
与椭圆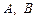 两点,
两点,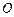 为坐标原点,若
为坐标原点,若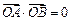 ,求
,求 的值。
的值。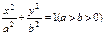 的离心率为
的离心率为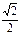 .
.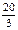 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;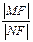 的值.
的值. y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求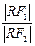 的值.
的值.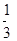 , -
, - )
)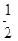 , -
, -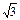 ,D是AB的中点.
,D是AB的中点. ·
·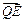 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值.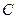 的顶点在原点,焦点F与双曲线
的顶点在原点,焦点F与双曲线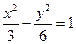 的右焦点重合,过点
的右焦点重合,过点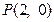 且斜率为1的直线
且斜率为1的直线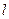 与抛物线
与抛物线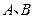 两点
两点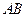 中点到抛物线准线的距离
中点到抛物线准线的距离