题目内容
(本小题满分13分)已知A,B分别是直线y=x和y=-x上的两个动点,线段AB的长为2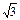 ,D是AB的中点.
,D是AB的中点.
(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
①当|PQ|=3时,求直线l的方程;
②设点E(m,0)是x轴上一点,求当 ·
·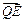 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值.
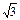 ,D是AB的中点.
,D是AB的中点.(1)求动点D的轨迹C的方程;
(2)若过点(1,0)的直线l与曲线C交于不同两点P、Q,
①当|PQ|=3时,求直线l的方程;
②设点E(m,0)是x轴上一点,求当
 ·
·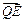 恒为定值时E点的坐标及定值.
恒为定值时E点的坐标及定值.解: (1)设D(x,y),A(a,a),B(b,-b),
∵ D是AB的中点, ∴x=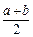 ,y=
,y=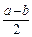 ,
,
∵ |AB|=2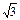 ,∴(a-b)2+(a+b)2=12,
,∴(a-b)2+(a+b)2=12,
∴(2y)2+(2x)2=12,∴点D的轨迹C的方程为x2+y2=3.
(2) ①当直线l与x轴垂直时,P(1, ),Q(1,-
),Q(1,- ),
),
此时|PQ|=2 ,不符合题意;
,不符合题意;
当直线l与x轴不垂直时,设直线l的方程为y=k(x-1),
由于|PQ|=3,所以圆心C到直线l的距离为 ,
,
由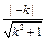 =
= ,解得k=
,解得k=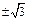 .故直线l的方程为y=
.故直线l的方程为y=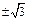 (x-1).
(x-1).
②当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1),
由消去y得(k2+1)x2-2k2x+k2-3=0,
设P(x1,y1),Q(x2,y2)则由韦达定理得x1+x2= ,x1x2=
,x1x2=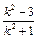 ,
,
则 =(m-x1,-y1),
=(m-x1,-y1),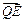 =(m-x2,-y2),
=(m-x2,-y2),
∴ ·
·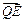 =(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2
=(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2
=m 2-m(x1+x2)+x1x2+k2(x1-1)(x2-1)
2-m(x1+x2)+x1x2+k2(x1-1)(x2-1)
=m2-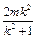 +
+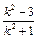 +k2 (
+k2 (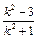 -
- +1)=
+1)=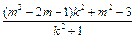
要使上式为定值须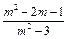 =1,解得m=1,
=1,解得m=1,
∴
 ·
·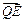 为定值-2,
为定值-2,
当直线l的斜率不存在时P(1, ),Q(1,-
),Q(1,- ),
),
由E(1,0)可得
 =(0,-
=(0,- ),
),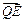 =(0,
=(0, ),
),
∴ ·
·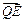 =-2,
=-2,
综上所述当E(1,0)时, ·
·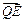 为定值-2.
为定值-2.
∵ D是AB的中点, ∴x=
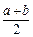 ,y=
,y=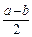 ,
,∵ |AB|=2
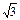 ,∴(a-b)2+(a+b)2=12,
,∴(a-b)2+(a+b)2=12,∴(2y)2+(2x)2=12,∴点D的轨迹C的方程为x2+y2=3.
(2) ①当直线l与x轴垂直时,P(1,
 ),Q(1,-
),Q(1,- ),
),此时|PQ|=2
 ,不符合题意;
,不符合题意;当直线l与x轴不垂直时,设直线l的方程为y=k(x-1),
由于|PQ|=3,所以圆心C到直线l的距离为
 ,
,由
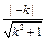 =
= ,解得k=
,解得k=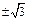 .故直线l的方程为y=
.故直线l的方程为y=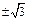 (x-1).
(x-1).②当直线l的斜率存在时,设其斜率为k,则l的方程为y=k(x-1),
由消去y得(k2+1)x2-2k2x+k2-3=0,
设P(x1,y1),Q(x2,y2)则由韦达定理得x1+x2=
 ,x1x2=
,x1x2=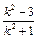 ,
,则
 =(m-x1,-y1),
=(m-x1,-y1),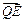 =(m-x2,-y2),
=(m-x2,-y2),∴
 ·
·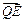 =(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2
=(m-x1)(m-x2)+y1y2=m2-m(x1+x2)+x1x2+y1y2=m
 2-m(x1+x2)+x1x2+k2(x1-1)(x2-1)
2-m(x1+x2)+x1x2+k2(x1-1)(x2-1)=m2-
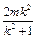 +
+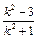 +k2 (
+k2 (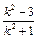 -
- +1)=
+1)=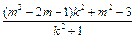
要使上式为定值须
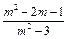 =1,解得m=1,
=1,解得m=1,∴

 ·
·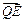 为定值-2,
为定值-2,当直线l的斜率不存在时P(1,
 ),Q(1,-
),Q(1,- ),
),由E(1,0)可得

 =(0,-
=(0,- ),
),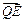 =(0,
=(0, ),
),∴
 ·
·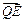 =-2,
=-2, 综上所述当E(1,0)时,
 ·
·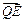 为定值-2.
为定值-2.略

练习册系列答案
相关题目
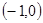 ,B
,B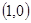 ,动点D,E满足:①
,动点D,E满足:①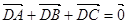 ;②
;②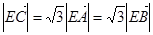 ,③
,③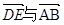 共线.
共线. 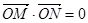 ,若存在,求该圆的方程;若不存在,请说明理由.
,若存在,求该圆的方程;若不存在,请说明理由.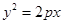 的焦点与椭圆
的焦点与椭圆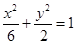 的右焦点重合,则
的右焦点重合,则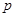 的值为 .
的值为 .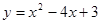 及其在点
及其在点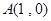 和
和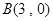 处的两条切线所围成图形的面积为
处的两条切线所围成图形的面积为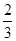
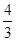
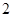

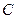 的方程为
的方程为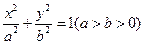 ,点
,点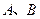 分别为其左、右顶点,点
分别为其左、右顶点,点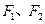 分别为其左、右焦点,以点
分别为其左、右焦点,以点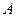 为圆心,
为圆心,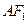 为半径作圆
为半径作圆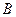 为圆心,
为圆心,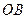 为半径作圆
为半径作圆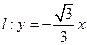 被圆
被圆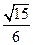 ;
;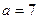 ,问是否存在点
,问是否存在点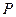 ,使得过
,使得过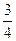 ;若存在,请求出所有的
;若存在,请求出所有的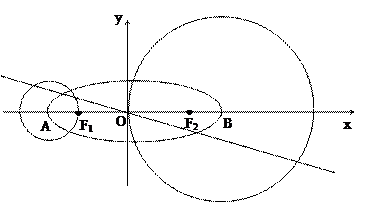
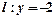 的距离小1.
的距离小1.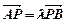 当△AOB的面积为
当△AOB的面积为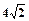 时(O为坐标原点),求的值.
时(O为坐标原点),求的值.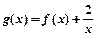 在[1,3]上是减函数,求实数a的取值范围.
在[1,3]上是减函数,求实数a的取值范围.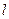 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线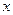 轴,
轴, 轴上滑动,M在线段AB上,且
轴上滑动,M在线段AB上,且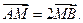
 且不垂直于坐标轴的动直线
且不垂直于坐标轴的动直线 交轨迹C于A、B两点,问:线段
交轨迹C于A、B两点,问:线段 上
上 恰有一个交点,则实数的b的取值范围是__________
恰有一个交点,则实数的b的取值范围是__________