题目内容
(本题满分16分)已知椭圆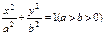 的离心率为
的离心率为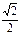 .
.
⑴若圆(x-2)2+(y-1)2=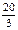 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
⑵设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600.求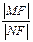 的值.
的值.
⑶在(1)的条件下,椭圆W的左右焦点分别为F1、 F2,点R在直线l:x- y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求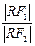 的值.
的值.
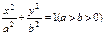 的离心率为
的离心率为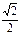 .
.⑴若圆(x-2)2+(y-1)2=
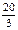 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;⑵设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600.求
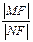 的值.
的值.⑶在(1)的条件下,椭圆W的左右焦点分别为F1、 F2,点R在直线l:x-
 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求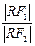 的值.
的值.解:(1)设A(x1,y1),B(x2,y2),AB的方程为y-1="k(x-2)" 即y=kx+1-2k①
∵离心率e=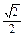
∴椭圆方程可化为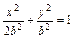 ②
②
将①代入②得(1+2k2)x2+4(1-2k)·kx
+2(1-2k)2-2b2=0
∵x1+x2=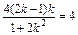 ∴k=-1
∴k=-1
∴x1x2=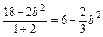
又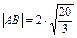
∴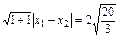 即
即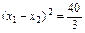
∴b2="8 "
∴椭圆方程为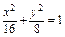
(2)设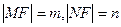 ,则由第二定义知
,则由第二定义知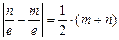 即
即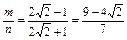 或
或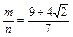
∴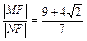 或
或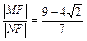 .
.
(3)当∠F1RF2取最大值时,过R、F1、F2的圆的圆心角最大,故其半径最小,与直线l相切.
直线l与x轴于S(-8,0),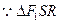 ∽
∽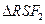 (可证)
(可证)
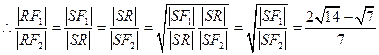
∵离心率e=
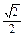
∴椭圆方程可化为
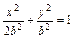 ②
②将①代入②得(1+2k2)x2+4(1-2k)·kx
+2(1-2k)2-2b2=0
∵x1+x2=
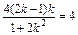 ∴k=-1
∴k=-1∴x1x2=
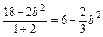
又
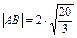
∴
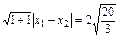 即
即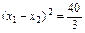
∴b2="8 "
∴椭圆方程为
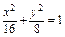
(2)设
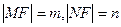 ,则由第二定义知
,则由第二定义知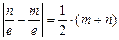 即
即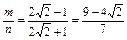 或
或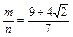
∴
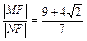 或
或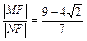 .
.(3)当∠F1RF2取最大值时,过R、F1、F2的圆的圆心角最大,故其半径最小,与直线l相切.
直线l与x轴于S(-8,0),
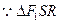 ∽
∽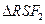 (可证)
(可证)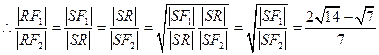
略

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
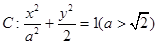 的左右焦点分别为F1,F2,A是椭圆C上第一象限内一点,
的左右焦点分别为F1,F2,A是椭圆C上第一象限内一点,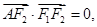 坐标原点O到直线AF1的距离为
坐标原点O到直线AF1的距离为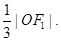
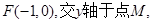 若
若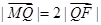 ,求直线l的斜率。
,求直线l的斜率。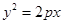 的焦点与椭圆
的焦点与椭圆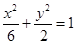 的右焦点重合,则
的右焦点重合,则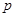 的值为 .
的值为 .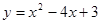 及其在点
及其在点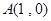 和
和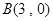 处的两条切线所围成图形的面积为
处的两条切线所围成图形的面积为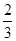
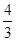
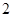

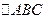 的两个顶点
的两个顶点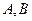 的坐标为
的坐标为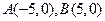 ,且
,且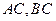 的斜率之积等于
的斜率之积等于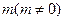 ,若顶点
,若顶点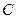 的轨迹是双曲线(去掉两个顶点),求
的轨迹是双曲线(去掉两个顶点),求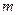 的取值范围.
的取值范围.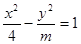 的渐近线方程为
的渐近线方程为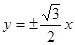 ,则双曲线的焦点坐标是
,则双曲线的焦点坐标是 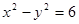 ”是“双曲线离心率
”是“双曲线离心率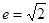 ”的 ( )
”的 ( )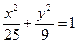 的左、右焦点为
的左、右焦点为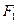 、
、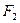 ,
,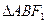 的顶点A、B在椭圆上,且边AB经过右焦点
的顶点A、B在椭圆上,且边AB经过右焦点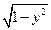 恰有一个交点,则实数的b的取值范围是__________
恰有一个交点,则实数的b的取值范围是__________