题目内容
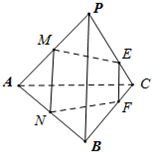
(本小题满分12分) 已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点,且PC⊥AB. (Ⅰ)求二面角P-AC-B的正切值; (Ⅱ)求点B到平面PAC的距离.
(Ⅰ) (Ⅱ)
(Ⅱ) 
 (Ⅱ)
(Ⅱ) 
:(Ⅰ)过 点作
点作 于
于 ,由正三棱柱性质知
,由正三棱柱性质知 平面
平面 ,连接
,连接 ,则
,则 为
为 在平面
在平面 上的射影.
上的射影.
 ,
,
 ,
,


 为
为 中点,又
中点,又 ,所以
,所以 为
为 的中点.过
的中点.过 作
作 于
于 ,连结
,连结 ,则
,则 ,
,

 为二面角
为二面角 的平面角
的平面角
在 中,由
中,由 =
= ,
, ,得
,得 .
.
所以二面角 的正切值为
的正切值为
(Ⅱ)
 是
是 中点,
中点,
 到平面
到平面 距离等于
距离等于 到平面
到平面 距离的2倍,又由(I)知
距离的2倍,又由(I)知 平面
平面 ,
,
 平面
平面
 平面
平面 ,
,
 过
过 作
作 于
于 ,则
,则 平面
平面 ,
,
 .故所求点
.故所求点 到平面
到平面 距离为
距离为
 点作
点作 于
于 ,由正三棱柱性质知
,由正三棱柱性质知 平面
平面 ,连接
,连接 ,则
,则 为
为 在平面
在平面 上的射影.
上的射影.
 ,
,
 ,
,

 为
为 中点,又
中点,又 ,所以
,所以 为
为 的中点.过
的中点.过 作
作 于
于 ,连结
,连结 ,则
,则 ,
,

 为二面角
为二面角 的平面角
的平面角在
 中,由
中,由 =
= ,
, ,得
,得 .
.所以二面角
 的正切值为
的正切值为
(Ⅱ)

 是
是 中点,
中点,
 到平面
到平面 距离等于
距离等于 到平面
到平面 距离的2倍,又由(I)知
距离的2倍,又由(I)知 平面
平面 ,
, 平面
平面
 平面
平面 ,
, 过
过 作
作 于
于 ,则
,则 平面
平面 ,
, .故所求点
.故所求点 到平面
到平面 距离为
距离为

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的8个顶点都在球O的表面上,则球O的表面积是 设
的8个顶点都在球O的表面上,则球O的表面积是 设 分别是该正方形的棱
分别是该正方形的棱 的中点,则直线
的中点,则直线 被球O截得的线段长为 .
被球O截得的线段长为 .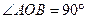 ,
,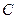 为空间中一点,且
为空间中一点,且 ,则直线
,则直线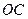 与平面
与平面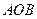 所成角
所成角 的正弦值为
的正弦值为 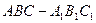 的所有棱长均为
的所有棱长均为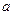 ,侧面
,侧面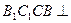 底面
底面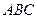 ,且
,且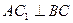 .
.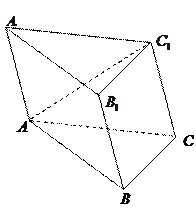
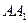 与
与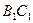 间的距离;
间的距离;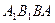 与底面
与底面 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ). 
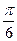



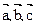 ,若
,若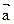 ∥
∥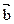 ,
,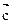 则
则