题目内容
如图,斜三棱柱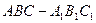 的所有棱长均为
的所有棱长均为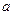 ,侧面
,侧面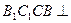 底面
底面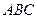 ,且
,且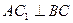 .
.
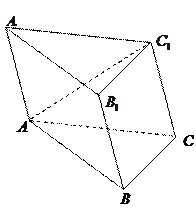
(1)求异面直线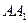 与
与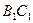 间的距离;
间的距离;
(2)求侧面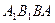 与底面
与底面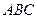 所成二面角的度数.
所成二面角的度数.
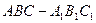 的所有棱长均为
的所有棱长均为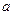 ,侧面
,侧面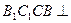 底面
底面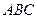 ,且
,且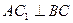 .
.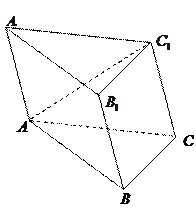
(1)求异面直线
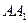 与
与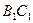 间的距离;
间的距离;(2)求侧面
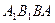 与底面
与底面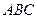 所成二面角的度数.
所成二面角的度数.(1) (2)
(2)
 (2)
(2)
(1)如图,取 中点D,连
中点D,连 .
.

 .
.
 ,∴
,∴ .
.
由 .……………4分
.……………4分
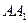 ∥
∥
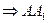 ∥平面
∥平面 .所以异面直线
.所以异面直线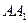 与
与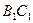 间的距离等于
间的距离等于
 .……………6分
.……………6分
(2)如图,

 ….8分
….8分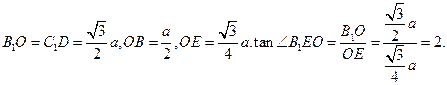
 .……………………12分
.……………………12分
 中点D,连
中点D,连 .
.
 .
.  ,∴
,∴ .
.由
 .……………4分
.……………4分 ∥
∥
 ∥平面
∥平面 .所以异面直线
.所以异面直线 与
与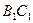 间的距离等于
间的距离等于
 .……………6分
.……………6分(2)如图,


 ….8分
….8分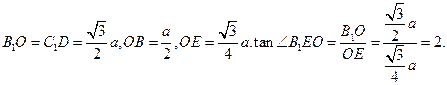
 .……………………12分
.……………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
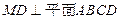 ,
,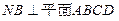 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点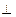 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由


 中,已知底面
中,已知底面 是边长为4的菱形,
是边长为4的菱形,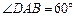 ,且点
,且点 在面
在面 与AC的交点O,设点E是
与AC的交点O,设点E是 的中点,
的中点,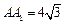 .
.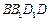 是矩形;
是矩形;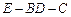 的大小;
的大小;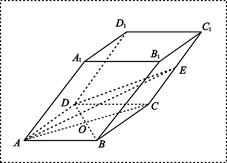 (Ⅲ) 求四面体
(Ⅲ) 求四面体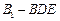 的体积.
的体积. 中,
中,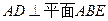 ,
,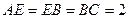 ,
,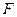 为
为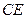 上的点,且
上的点,且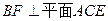 .
.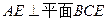 ;(Ⅱ)求证;
;(Ⅱ)求证;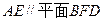 ;
;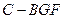 的体积.
的体积.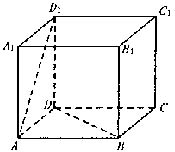 如图,正方体ABCD—A1B1C1D1的棱长为1,PQ分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12.
如图,正方体ABCD—A1B1C1D1的棱长为1,PQ分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12. 上的函数
上的函数 ,其中
,其中 为常数.
为常数. ,求证:函数
,求证:函数 在区间
在区间 上是增函数;
上是增函数; ,在
,在 处取得最大值,求正数
处取得最大值,求正数 在同一个球面上,
在同一个球面上,  平面
平面 ,
, ,若
,若 ,
,
 ,
, ,则
,则 两点间的球面距离是 .
两点间的球面距离是 . 是球心
是球心 的半径
的半径 上的两点,且
上的两点,且 ,分别过
,分别过 作垂线于
作垂线于 B、
B、 C、
C、 D、
D、