题目内容
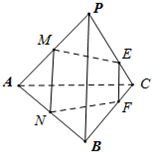
三棱锥P-ABC中M、N分别是AP、AB的中点,
=
=2下列命题正确的是( )
| PE |
| EC |
| BF |
| FC |
| A.MN=EF |
| B.ME与NF是异面直线 |
| C.直线ME、NF、AC相交于同一点 |
| D.直线ME、NF、AC不相交于同一点 |

∵M、N分别是AP、AB的中点,
∴MN∥PB,且MN=
PB
又由
=
=2
∴EF∥PB,且EF=
PB
∴MN∥EF,且MN≠EF
∴四边形MNFE为梯形
∴ME与NF必交于一点
又由ME?平面APC
NF?平面ABC
平面APC∩平面ABC=AC
由公理3易得,ME与NF交点在直线AC上
故直线ME、NF、AC相交于同一点
故选C
∴MN∥PB,且MN=
| 1 |
| 2 |
又由
| PE |
| EC |
| BF |
| FC |
∴EF∥PB,且EF=
| 1 |
| 3 |
∴MN∥EF,且MN≠EF
∴四边形MNFE为梯形
∴ME与NF必交于一点
又由ME?平面APC
NF?平面ABC
平面APC∩平面ABC=AC
由公理3易得,ME与NF交点在直线AC上
故直线ME、NF、AC相交于同一点
故选C

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图,在四棱锥P-ABCD中,
如图,在四棱锥P-ABCD中,
 为正三角形,且平面PAD⊥平面ABCD.网
为正三角形,且平面PAD⊥平面ABCD.网 的重心,求二面角G-BD-C大小.
的重心,求二面角G-BD-C大小.








 (2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1
(2)平面AB1D与侧面BB1C1C所成锐角的大小 C1 B1 是球心
是球心 的半径
的半径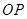 上的两点,且
上的两点,且 ,分别过
,分别过 作垂线于
作垂线于 B、
B、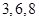 C、
C、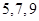 D、
D、