题目内容
如图,是一个无盖正方体盒子的表面展开图, 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ).
 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ).
|
A.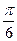 | B. | C. | D. |
C
把展开图还原可以得到:在正方体中三角形ABC是等边三角形,所以
 .
.

 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ).
|
A.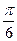 | B. | C. | D. |

 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案