题目内容
12. 如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
分析 以A为坐标原点,AB,AC所在直线为y,x轴,建立直角坐标系,即有A(0,0),B(0,4),C(2,0),设D(a,b),E(c,d),F(e,f),由向量共线的坐标表示,解方程可得D,E,F,再由向量的数量积的坐标表示,计算即可得到.
解答 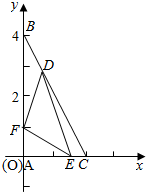 解:以A为坐标原点,AB,AC所在直线为y,x轴,建立直角坐标系,
解:以A为坐标原点,AB,AC所在直线为y,x轴,建立直角坐标系,
即有A(0,0),B(0,4),C(2,0),设D(a,b)
E(c,d),F(e,f),
由$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则(c-2,d-0)=$\frac{1}{4}$(-2,0),
(e,f)=$\frac{1}{4}$(0,4),(a,b-4)=$\frac{1}{4}$(2,-4),
解得D($\frac{1}{2}$,3),E($\frac{3}{2}$,0),F(0,1),
即有$\overrightarrow{DE}$=(1,-3),$\overrightarrow{DF}$=(-$\frac{1}{2}$,-2),
则$\overrightarrow{DE}$•$\overrightarrow{DF}$=1×(-$\frac{1}{2}$)+(-3)×(-2)=$\frac{11}{2}$.
故答案为:$\frac{11}{2}$.
点评 本题考查向量的数量积的坐标表示,主要考查向量共线的坐标运算,注意运用坐标法是解题的关键.

练习册系列答案
相关题目
7.已知b,c∈R,函数f(x)=x2+bx+c,方程f(x)-x=0的两个实根为x1,x2,且x2-x1>2,若四次方程f(f(x))=x的另两个根为x3,x4(其中x3<x4),则( )
| A. | x1<x2<x3<x4 | B. | x3<x1<x4<x2 | C. | x1<x3<x4<x2 | D. | x1<x3<x2<x4 |