题目内容

20．求${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx的值．

分析 ${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx的几何意义是表示y=$\sqrt{9-{x}^{2}}$与x轴，x=0，x=3所围成的图形的面积，可求．

解答 解：${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx的几何意义是表示y=$\sqrt{9-{x}^{2}}$与x轴，x=0，x=3所围成的图形的面积，
因为y=$\sqrt{9-{x}^{2}}$是以原点为圆心，以3为半径的圆的上半部分，
所以${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx以原点为圆心，以3为半径的圆的面积的$\frac{1}{4}$，
∴${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx=$\frac{1}{4}×9π=\frac{9π}{4}$．

点评 本题主要考查了定积分的几何意义的应用，解题的关键是确定被积函数所确定的图形．

练习册系列答案
相关题目
10．已知等差数列{an}中，a2+a9=a6，则其前9项和S9的值为（　　）
A．-2B．0C．1D．-2
11．若$\frac{3sinα-cosα}{sinα+3cosα}$=1，求：
（1）tanα的值；
（2）$\frac{sinα+cosα}{sinα-cosα}$+cos2α的值．
8．已知f（x）=lnx-ax2-bx．记f（x）的导函数是f′（x）．
（Ⅰ）若a=-1，函数f（x）在其定义域内是增函数，求b的取值范围；
（Ⅱ） f（x）的图象与x轴交于A（x1，0），B（x2，0）（x1＜x2））两点，AB中点为C（x0，0），求证：f′（x0）＜0．
15．已知x∈R，a＜lg（|x-3|+|x+7|）恒成立，则a的取值范围是（　　）
A．a≥1B．a＞1C．a≤1D．a＜1
5．水平放置棱长为2的正方体，以其各面中心为顶点的几何体的正、侧、俯视图的面积不可能为（　　）
A．4B．2C．$\frac{{\sqrt{2}+\sqrt{6}}}{2}$D．$\sqrt{2}$
12．如图，在△ABC中，|$\overrightarrow{AB}$|=4，|$\overrightarrow{AC}$|=2，∠BAC=90°，D，E，F分别是边BC，CA，AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$，$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$，$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$，则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$．
10．已知O为坐标原点，F为抛物线C：y2=4$\sqrt{6}$x的焦点，P为C上一点，若△POF的面积为6$\sqrt{3}$，则|PF|=（　　）
A．$2\sqrt{3}$B．$4\sqrt{3}$C．$4\sqrt{6}$D．$8\sqrt{3}$
11．如图，在公路MN的两侧有四个村镇：A1、B1、C1、D1通过小路和公路相连，各路口分别是A、B、C、D，现要在公路上建一个长途汽车站，为使各村镇村民到汽车站所走的路程总和最小，汽车站应建在（　　）
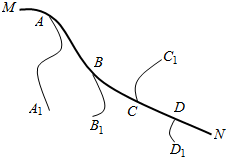
A．A处B．D处
C．B、C间的任何一处（包括B、C）D．A、B之间的任何一处（包括A、B）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网