题目内容
5.已知椭圆C的两焦点为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),长轴长是短轴长的2倍.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点(1,0)的直线l与椭圆C交于M(x1,y1),N(x2,y2)两点,若x1x2+y1y2=0,求直线l的方程.
分析 (Ⅰ)由题意可得a=2b,a,b,c的关系,计算即可得到a,b,进而得到椭圆方程;
(Ⅱ)设直线l的方程为y=k(x-1),代入椭圆方程,运用韦达定理,化简整理即可得到k,进而得到所求直线方程.
解答 解:(Ⅰ)由已知$\left\{\begin{array}{l}a=2b\;,\;\\ c=\sqrt{3}\;\\{a^2}={b^2}+{c^2}\;,\;\;\end{array}\right.$
解得a2=4,b2=1,
所以椭圆的方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)设直线l的方程为y=k(x-1),
由$\left\{\begin{array}{l}{x^2}+4{y^2}=4\;,\;\\ y=k(x-1)\;,\;\end{array}\right.$消去y,得(1+4k2)x2-8k2x+4k2-4=0,
所以${x_1}+{x_2}=\frac{{8{k^2}}}{{1+4{k^2}}}$,${x_1}•{x_2}=\frac{{4({k^2}-1)}}{{1+4{k^2}}}$.
${x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+{k^2}({x_1}-1)({x_2}-1)=(1+{k^2}){x_1}{x_2}-{k^2}({x_1}+{x_2})+{k^2}$
=$\frac{{4(1+{k^2})({k^2}-1)}}{{1+4{k^2}}}-\frac{{8{k^4}}}{{1+4{k^2}}}+{k^2}=\frac{{{k^2}-4}}{{1+4{k^2}}}$=0,
所以k2-4=0,解得k=±2.
所以直线l的方程为y=2x-2或y=-2x+2.
点评 本题考查椭圆的方程和性质,主要考查椭圆的方程和运用,联立直线方程,运用韦达定理,考查化简整理和运算求解能力,属于中档题.

| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<1 |
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 用水量y | 2.5 | 3 | 4 | 4.5 | 5.2 |
(2)从这5个月中任取2个月的用水量,求所取2个月的用水灵之和不超过7(单位:百吨)的概率.
| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $4\sqrt{6}$ | D. | $8\sqrt{3}$ |
| A. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D. | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
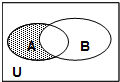 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )| A. | {x|x>1} | B. | {x|1<x≤$\frac{4}{3}$} | C. | {x|x≤1} | D. | {x|x>$\frac{4}{3}$} |
 如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$. 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.