在平面直角坐标系xOy中.设D={(x.y)|$\left\{\begin{array}{l}{x+y-1≤0}\\{x-y+1≥0}\\{y≥0}\end{array}\right.$}.E={(x.y)|x2+y2≤1}.若向E中随机投一点.则所投点落在D中的概率是$\frac{1}{π}$．题目和参考答案——青夏教育精英家教网—

题目内容

3．在平面直角坐标系xOy中，设D={（x，y）|$\left\{\begin{array}{l}{x+y-1≤0}\\{x-y+1≥0}\\{y≥0}\end{array}\right.$}，E={（x，y）|x²+y²≤1}，若向E中随机投一点，则所投点落在D中的概率是$\frac{1}{π}$．

分析作出不等式组对应的平面区域，根据几何概型的概率公式求出对应事件的面积即可得到结论．

解答解：作出对应的图象如图：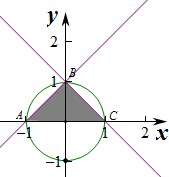
则△ABC的面积S=$\frac{1}{2}×2×1=1$，
则对应的概率P=$\frac{{S}_{△ABC}}{{S}_{圆}}$=$\frac{1}{π×{1}^{2}}$=$\frac{1}{π}$，
故答案为：$\frac{1}{π}$．

点评本题主要考查几何概型的概率计算，根据条件求出对应区域的面积是解决本题的关键．

练习册系列答案

永乾教育暑假作业快乐假期延边人民出版社系列答案

14．在等差数列{a_n}中，
（1）已知d=3，a_n=20，S_n=65，求n；
（2）已知a₁₁=-1，求S₂₁；
（3）已知a_n=11-3n，求S_n．

11．若$\frac{3sinα-cosα}{sinα+3cosα}$=1，求：
（1）tanα的值；
（2）$\frac{sinα+cosα}{sinα-cosα}$+cos²α的值．

18．已知函数f（x）=lnx-mx²，g（x）=$\frac{1}{2}$mx²+x（m∈R），令F（x）=f（x）+g（x）．
（1）若函数f（x）在（0，1）上单调递增，求实数m的取值范围；
（2）若过原点O可作曲线y=f（x）的两条切线，求实数m的取值范围；
（3）若关于x的不等式F（x）≤mx-1恒成立，求整数m的最小值．

8．已知f（x）=lnx-ax²-bx．记f（x）的导函数是f′（x）．
（Ⅰ）若a=-1，函数f（x）在其定义域内是增函数，求b的取值范围；
（Ⅱ） f（x）的图象与x轴交于A（x₁，0），B（x₂，0）（x₁＜x₂））两点，AB中点为C（x₀，0），求证：f′（x₀）＜0．

15．已知x∈R，a＜lg（|x-3|+|x+7|）恒成立，则a的取值范围是（　　）

12．

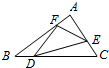如图，在△ABC中，|$\overrightarrow{AB}$|=4，|$\overrightarrow{AC}$|=2，∠BAC=90°，D，E，F分别是边BC，CA，AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$，$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$，$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$，则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$．

14．若曲线C上的点到椭圆 $\frac{{x}^{2}}{1{3}^{2}}$+$\frac{{y}^{2}}{1{2}^{2}}$=1的两个焦点的距离的差的绝对值等于8，则曲线C的标准方程为（　　）

	A．	$\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1		B．	$\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1
	C．	$\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1		D．	$\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1

试题分类