题目内容
2.已知函数f(x)=ax2+2x-lnx(a∈R).(Ⅰ)若a=4,求函数f(x)的极值;
(Ⅱ)若f′(x)在(0,1)有唯一的零点x0,求a的取值范围;
(Ⅲ)若a∈(-$\frac{1}{2}$,0),设g(x)=a(1-x)2-2x-1-ln(1-x),求证:g(x)在(0,1)内有唯一的零点x1,且对(Ⅱ)中的x0,满足x0+x1>1.
分析 解法一:(Ⅰ)当a=4时,化简函数的解析式,求出定义域,函数的导数,求出极值点,利用导函数的符号判断函数的单调性,求解极值即可.
(Ⅱ)利用$f'(x)=2ax+2-\frac{1}{x}=\frac{{2a{x^2}+2x-1}}{x}$,通过导函数为0,构造新函数,通过分类讨论求解即可.
(Ⅲ)设t=1-x,则t∈(0,1),得到p(t),求出函数的导数$p'(t)=2at+2-\frac{1}{t}=\frac{{2a{t^2}+2t-1}}{t}$,通过方程2at2+2t-1=0在(0,1)内有唯一的解x0,利用导数判断单调性,然后求解证明.
解法二:(Ⅰ)同解法一;
(Ⅱ)求出$f'(x)=2ax+2-\frac{1}{x}=\frac{{2a{x^2}+2x-1}}{x}$,通过f′(x)=0,推出$a=\frac{1}{{2{x^2}}}-\frac{1}{x}$,设$m=\frac{1}{x}$,则m∈(1,+∞),问题转化为直线y=a与函数$h(m)=\frac{1}{2}{(m-1)^2}-\frac{1}{2}$的图象在(1,+∞)恰有一个交点问题.
求解证明即可.
(Ⅲ)同解法一.
解答 满分(14分).
解法一:(Ⅰ)当a=4时,f(x)=4x2+2x-lnx,x∈(0,+∞),$f'(x)=8x+2-\frac{1}{x}=\frac{{8{x^2}+2x-1}}{x}=\frac{(4x-1)(2x+1)}{x}$.…(1分)
由x∈(0,+∞),令f′(x)=0,得$x=\frac{1}{4}$.
当x变化时,f′(x),f(x)的变化如下表:
| x | $(0,\frac{1}{4})$ | $\frac{1}{4}$ | $(\frac{1}{4},+∞)$ |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
(Ⅱ)$f'(x)=2ax+2-\frac{1}{x}=\frac{{2a{x^2}+2x-1}}{x}$,
令f′(x)=0,得2ax2+2x-1=0,设h(x)=2ax2+2x-1.
则f′(x)在(0,1)有唯一的零点x0等价于h(x)在(0,1)有唯一的零点x0
当a=0时,方程的解为$x=\frac{1}{2}$,满足题意;…(5分)
当a>0时,由函数h(x)图象的对称轴$x=-\frac{1}{2a}<0$,函数h(x)在(0,1)上单调递增,
且h(0)=-1,h(1)=2a+1>0,所以满足题意;…(6分)
当a<0,△=0时,$a=-\frac{1}{2}$,此时方程的解为x=1,不符合题意;
当a<0,△≠0时,由h(0)=-1,
只需h(1)=2a+1>0,得$-\frac{1}{2}<a<0$.…(7分)
综上,$a>-\frac{1}{2}$.…(8分)
(说明:△=0未讨论扣1分)
(Ⅲ)设t=1-x,则t∈(0,1),p(t)=g(1-t)=at2+2t-3-lnt,…(9分)$p'(t)=2at+2-\frac{1}{t}=\frac{{2a{t^2}+2t-1}}{t}$,
由$a∈(-\frac{1}{2},0)$,故由(Ⅱ)可知,
方程2at2+2t-1=0在(0,1)内有唯一的解x0,
且当t∈(0,x0)时,p′(t)<0,p(t)单调递减;t∈(x0,1)时,p′(t)>0,p(t)单调递增.…(11分)
又p(1)=a-1<0,所以p(x0)<0.…(12分)
取t=e-3+2a∈(0,1),
则p(e-3+2a)=ae-6+4a+2e-3+2a-3-lne-3+2a=ae-6+4a+2e-3+2a-3+3-2a=a(e-6+4a-2)+2e-3+2a>0,
从而当t∈(0,x0)时,p(t)必存在唯一的零点t1,且0<t1<x0,
即0<1-x1<x0,得x1∈(0,1),且x0+x1>1,
从而函数g(x)在(0,1)内有唯一的零点x1,满足x0+x1>1.…(14分)
解法二:(Ⅰ)同解法一;…(4分)
(Ⅱ)$f'(x)=2ax+2-\frac{1}{x}=\frac{{2a{x^2}+2x-1}}{x}$,
令f′(x)=0,由2ax2+2x-1=0,得$a=\frac{1}{{2{x^2}}}-\frac{1}{x}$.…(5分)
设$m=\frac{1}{x}$,则m∈(1,+∞),$a=\frac{1}{2}{m^2}-m=\frac{1}{2}{(m-1)^2}-\frac{1}{2}$,…(6分)
问题转化为直线y=a与函数$h(m)=\frac{1}{2}{(m-1)^2}-\frac{1}{2}$的图象在(1,+∞)恰有一个交点问题.
又当m∈(1,+∞)时,h(m)单调递增,…(7分)
故直线y=a与函数h(m)的图象恰有一个交点,当且仅当$a>-\frac{1}{2}$.…(8分)
(Ⅲ)同解法一.
(说明:第(Ⅲ)问判断零点存在时,利用t→0时,p(t)→+∞进行证明,扣1分)
点评 本题考查函数与导数等基本知识,考查推理论证能力和运算求解能力,考查函数与方程的思想、化归与转化的思想、数形结合的思想,考查运用数学知识分析和解决问题的能力.

| A. | $2\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $4\sqrt{6}$ | D. | $8\sqrt{3}$ |
| A. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D. | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
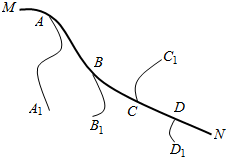
| A. | A处 | B. | D处 | ||
| C. | B、C间的任何一处(包括B、C) | D. | A、B之间的任何一处(包括A、B) |
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
 如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$. 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.