题目内容
已知△ABC的三顶点A(3,-1),B(9,5),C(2,6).
(1)求边AB上的中线所在直线的方程;
(2)求角B的平分线所在直线的方程.
(1)求边AB上的中线所在直线的方程;
(2)求角B的平分线所在直线的方程.
(1)设AB边的中点为M,则M(6,2)
∴直线CM方程是:
=
即:x+y-8=0.
(2)设角B的平分线所在直线的斜率为k,
依题意得:kAB=1,kBC=-
=
⇒k=
或k=-3(舍).
故角B的平分线所在直线的方程是:x-3y+6=0.
∴直线CM方程是:
| y-2 |
| 6-2 |
| x-6 |
| 2-6 |
即:x+y-8=0.
(2)设角B的平分线所在直线的斜率为k,
依题意得:kAB=1,kBC=-
| 1 |
| 7 |
| kAB-k |
| 1+kkAB |
| k-kBC |
| 1+kkBC |
| 1 |
| 3 |
故角B的平分线所在直线的方程是:x-3y+6=0.

练习册系列答案
相关题目
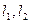 的倾斜角分别是
的倾斜角分别是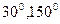 ,点A在
,点A在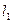 上,点B在
上,点B在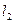 上,且
上,且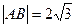 ,(1)若P为线段AB的中点,求点P的轨迹方程(2)若P为线段AB的中点, 定点
,(1)若P为线段AB的中点,求点P的轨迹方程(2)若P为线段AB的中点, 定点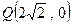 ,且
,且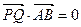 ,求点P
,求点P