题目内容
△ABC中,C(3,-1),AC边上的高线方程为x-2y+2=0,BC边上的中线方程为7x-y-4=0,求AB,BC,AC边所在的直线方程.
∵AC边上的高线方程为x-2y+2=0
∴高线的斜率为
,由垂直关系可得kAC=-2,
∴直线AC的点斜式方程为:y+1=-2(x-3),
化为一般式可得:2x+y-5=0;
联立方程组
,
解得
,可得A(1,3)
设B(x,y),
则BC的中点为(
,
),
由
,
解得
,可得B(-2,0)
∴直线BC的斜率为kBC=
=-
,
∴BC的方程为:y-0=-
(x+2),
化为一般式可得x+5y+2=0
同理可得直线AB的斜率kAB=
=1,
∴直线AB方程为y-0=x+2,
化为一般式可得:x-y+2=0
∴高线的斜率为
| 1 |
| 2 |
∴直线AC的点斜式方程为:y+1=-2(x-3),
化为一般式可得:2x+y-5=0;
联立方程组
|
解得
|
设B(x,y),
则BC的中点为(
| x+3 |
| 2 |
| y-1 |
| 2 |
由
|
解得
|
∴直线BC的斜率为kBC=
| -1-0 |
| 3-(-2) |
| 1 |
| 5 |
∴BC的方程为:y-0=-
| 1 |
| 5 |
化为一般式可得x+5y+2=0
同理可得直线AB的斜率kAB=
| 3-0 |
| 1-(-2) |
∴直线AB方程为y-0=x+2,
化为一般式可得:x-y+2=0

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
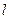 过点P(2,3),并与
过点P(2,3),并与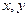 轴正半轴交于A,B二点。
轴正半轴交于A,B二点。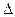 AOB面积为
AOB面积为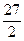 时,求直线
时,求直线