题目内容
直线
(t2+1)x+2ty+1=0的倾斜角的范围是( )
| 3 |
| A.[0,π) | B.[
| ||||||||
C.[
| D.[0,
|
因为
(t2+1)x+2ty+1=0,所以当t=0时,直线的斜率不存在,直线的倾斜角为:
,
当直线的斜率存在时,t≠0,直线的斜率k=-
=-
(t+
),
当t>0时,
(t+
)≥
,直线的倾斜角的范围是(
,
],
当t<0时,
(t+
)≤-
,直线的倾斜角的范围是[
,
),
综上,直线的倾斜角的范围是:[
,
]
故选C.
| 3 |
| π |
| 2 |
当直线的斜率存在时,t≠0,直线的斜率k=-
| ||
| 2t |
| ||
| 2 |
| 1 |
| t |
当t>0时,
| ||
| 2 |
| 1 |
| t |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
当t<0时,
| ||
| 2 |
| 1 |
| t |
| 3 |
| π |
| 3 |
| π |
| 2 |
综上,直线的倾斜角的范围是:[
| π |
| 3 |
| 2π |
| 3 |
故选C.

练习册系列答案
相关题目
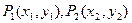 分别是直线
分别是直线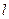 上和直线
上和直线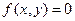 ,则方程
,则方程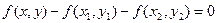 表示
表示