题目内容

11．已知函数f（x）=（2a-1）x+b在（-∞，+∞）上是减函数，则实数a的取值范围是（-∞，$\frac{1}{2}$）（用区间表示）．

分析 根据f（x）为减函数及一次函数的单调性便可得出2a-1＜0，这样便可得出实数a的取值范围．

解答 解：f（x）在（-∞，+∞）上为减函数；
∴f（x）为一次函数，2a-1＜0；
∴$a＜\frac{1}{2}$；
∴实数a的取值范围为（-∞，$\frac{1}{2}$）．
故答案为：$（-∞，\frac{1}{2}）$．

点评 考查减函数的定义，以及一次函数的单调性．

练习册系列答案
相关题目
18．已知向量$\overrightarrow{a}$=（x0-2，y0），向量$\overrightarrow{b}$=（x0+2，y0），且|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=4$\sqrt{3}$，设M（x0，y0），A（-2，0），B（2，0），则|$\overrightarrow{MA}$|•|$\overrightarrow{MB}$|的最大值为（　　）
A．4B．6C．8D．12
2．已知0＜θ＜π，且sinθ-cosθ=$\frac{1}{5}$，求sinθ+cosθ，tanθ的值．
19．函数f（x）对任意a，b∈R，有f（a+b）=f（a）+f（b）-1，且当x＞0时，f（x）＞1．
（Ⅰ）求证：f（x）是R 上的增函数；
（Ⅱ）若f（-4）=5，解不等式f（3m2-m-3）＜2．
6．已知函数f（x）=$\frac{a{x}^{2}+1}{bx+c}$（a，b，c∈Z）是奇函数，且f（1）=2，f（2）＜3．
（1）求a，b，c的值．
（2）判断函数f（x）在[1，+∞）上的单调性，并用定义证明你的结论．
（3）解关于t的不等式：f（-t2-1）+f（|t|+3）＞0．
16．若6＜a＜10，$\frac{a}{2}$≤b≤2a，c=a+b，那么c的取值范围是（　　）
A．9≤c≤18B．15＜c＜30C．9≤c≤30D．9＜c＜30
3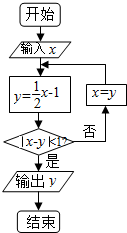．执行如图所示的程序框图，若输入x的值为4，则输出的结果是（　　）
A．1B．$-\frac{1}{2}$C．$-\frac{5}{4}$D．$-\frac{13}{8}$
20．已知函数f（x）=$\sqrt{3}$sin（2x+$\frac{π}{3}$）+cos（2x+$\frac{π}{3}$）．
（Ⅰ）求f（$\frac{π}{6}$）的值；
（Ⅱ）求函数f（x）的最小正周期和单调递增区间．
1．已知Sn为等差数列{an}的前n项和，且a2=4，S4=20．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$，求数列{bn}的前n项和．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网