题目内容
19.函数f(x)对任意a,b∈R,有f(a+b)=f(a)+f(b)-1,且当x>0时,f(x)>1.(Ⅰ)求证:f(x)是R 上的增函数;
(Ⅱ)若f(-4)=5,解不等式f(3m2-m-3)<2.
分析 (Ⅰ)设实数x1<x2,则x2-x1>0,利用已知可得f(x2-x1)>1.再利用已知可得f(x2)=f(x2-x1+x1)=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1)即可;
(Ⅱ)令a=b=-2,以及a=b=-1,解得f(-2)=3,f(-1)=2,不等式f(3m2-m-3)<2.化为f(3m2-m-3)<f(-1),由(1)可得:f(x)在R上是增函数.可得3m2-m-3<-1,解得即可.
解答 解:(Ⅰ)证明:设x1<x2,则x2-x1>0,
∵当x>0时,f(x)>1,∴f(x2-x1)>1.
又函数f(x)对任意a,b∈R都有f(a+b)=f(a)+f(b)-1,
∴f(x2)=f(x2-x1+x1)=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),
∴f(x2)>f(x1),
∴f(x)在R上是增函数;
(Ⅱ)令a=b=-2,则f(-2-2)=f(-2)+f(-2)-1=5,解得f(-2)=3,
再令a=b=-1,则f(-1-1)=f(-1)+f(-1)-1=3,解得f(-1)=2.
不等式f(3m2-m-3)<2.化为f(3m2-m-3)<f(-1).
由(1)可得:f(x)在R上是增函数.
∴3m2-m-3<-1,解得-$\frac{2}{3}$<m<1.
∴不等式f(3m2-m-3)<2的解集为(-$\frac{2}{3}$,1).
点评 本题考查了抽象函数的单调性、求值、解不等式等基础知识与基本方法,考查了灵活应用知识解决问题的能力,属于中档题.

练习册系列答案
相关题目
7.若f(x)=x+$\frac{1}{x}$,则下列式子中正确的是( )
| A. | f(-1)=0 | B. | f(0)=0 | C. | f(-x)=f(x) | D. | f($\frac{1}{x}$)=f(x) |
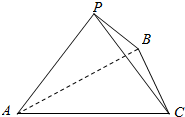 如图,三棱锥P-ABC的底面是边长为2的等边三角形.若PA=PB=$\sqrt{2}$.二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$.
如图,三棱锥P-ABC的底面是边长为2的等边三角形.若PA=PB=$\sqrt{2}$.二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$.