题目内容
16.若6<a<10,$\frac{a}{2}$≤b≤2a,c=a+b,那么c的取值范围是( )| A. | 9≤c≤18 | B. | 15<c<30 | C. | 9≤c≤30 | D. | 9<c<30 |
分析 由c=a+b,$\frac{a}{2}$≤b≤2a,得$\frac{3a}{2}$≤c≤3a,然后根据a的取值范围得出答案.
解答 解:∵$\frac{a}{2}$≤b≤2a,
∴$\frac{3a}{2}$≤a+b≤3a
即$\frac{3a}{2}$≤c≤3a
∵6<a<10,
∴9<c<30.
故选D.
点评 本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
3.在首项为负数的等差数列{an}中,若a10+a11+a12=0,则当数列{an}的前n项和Sn取最小值时,n等于.
| A. | 10 | B. | 10或11 | C. | 11 | D. | 9或10 |
1.过点A(-2,3)作直线与抛物线y2=8x在第一象限相切于点B,记抛物线的焦点为F,则直线BF的斜率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
6.函数f(x)=ax(a>0且a≠1)在区间[1,2]上的最大值比最小值大$\frac{a}{4}$,则实数a的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}或\frac{5}{4}$ | D. | $\frac{3}{4}或\frac{5}{4}$ |
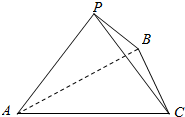 如图,三棱锥P-ABC的底面是边长为2的等边三角形.若PA=PB=$\sqrt{2}$.二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$.
如图,三棱锥P-ABC的底面是边长为2的等边三角形.若PA=PB=$\sqrt{2}$.二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的半径=$\frac{\sqrt{13}}{3}$.