题目内容
3.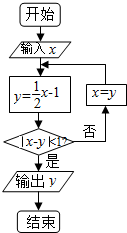 执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )
执行如图所示的程序框图,若输入x的值为4,则输出的结果是( )| A. | 1 | B. | $-\frac{1}{2}$ | C. | $-\frac{5}{4}$ | D. | $-\frac{13}{8}$ |
分析 根据程序框图依次计算框图运行的x、y值,直到满足条件|y-x|<1终止运行,输出y值.
解答 解:由程序框图得第一次运行y=$\frac{1}{2}$×4-1=1,
第二次运行x=1,y=$\frac{1}{2}$×1-1=-$\frac{1}{2}$,
第三次运行x=-$\frac{1}{2}$,y=$\frac{1}{2}$×(-$\frac{1}{2}$)-1=-$\frac{5}{4}$,此时|y-x|=$\frac{3}{4}$,满足条件|y-x|<1终止运行,输出-$\frac{5}{4}$.
故选:C.
点评 本题是直到型循环结构的程序框图,解答的关键是读懂框图的运行流程,属于基础题.

练习册系列答案
相关题目
15.函数f(x)=$\left\{\begin{array}{l}a{x^2}+x-1(x>2)\\ ax-1(x≤2)\end{array}$是R上的单调递减函数,则实数a的取值范围是( )
| A. | -$\frac{1}{4}$≤a<0 | B. | a≤-$\frac{1}{4}$ | C. | -1≤a≤-$\frac{1}{4}$ | D. | a≤-1 |