Question

19．在平面直角坐标系中，若$\left\{\begin{array}{l}{x≤2}\\{|y-2|≤x}\end{array}\right.$，则（x+1）²+y²的取值范围是（　　）

• A． [$\sqrt{5}$，5]
• B． [$\frac{3\sqrt{2}}{2}$，5]
• C． [$\frac{9}{2}$，25]
• D． [9，25]

Answer 1

分析 由题意作出其平面区域，（x+1）²+y²可看成阴影内的点到点A（-1，0）的距离的平方，求阴影内的点到点A（-1，0）的距离的范围可得．

解答 解：由题意作出其平面区域，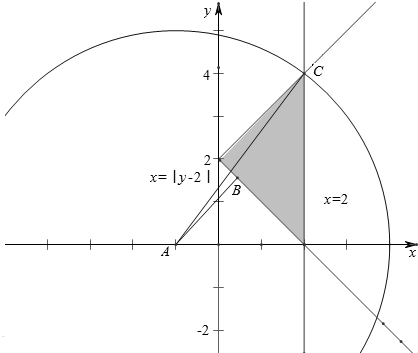

（x+1）²+y²可看成阴影内的点到点A（-1，0）的距离的平方，
由图象可得，
AB=3×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{2}}{2}$，AC=$\sqrt{{3}^{2}+{4}^{2}}$=5；
故（$\frac{3\sqrt{2}}{2}$）²≤（x+1）²+y²≤25，
即$\frac{9}{2}$≤（x+1）²+y²≤25；
故选C．

点评 本题考查了简单线性规划，作图要细致认真，用到了表达式的几何意义的转化，属于中档题．