题目内容
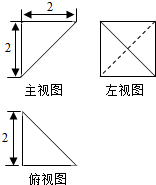
7. 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的表面积是( )| A. | 16$\sqrt{2}$+16π | B. | 16$\sqrt{2}$+8π | C. | 8$\sqrt{2}$+8π | D. | 8$\sqrt{2}$+16π |
分析 几何体是半圆锥,根据三视图的数据判断底面半径与高,求母线长,把数据代入表面积公式计算.
解答 解:由三视图知:几何体是半圆锥,
其中底面半径为2,高为4$\sqrt{2}$.∴母线长为6.
∴几何体的表面积S=$\frac{1}{2}$π×22+$\frac{1}{2}$×4×4$\sqrt{2}$+$\frac{1}{2}$×π×2×6=8π+8$\sqrt{2}$.
故选:C.
点评 本题考查了由三视图求几何体的表面积,根据三视图判断几何体的形状及数据所对应的几何量是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
12.已知顶点为坐标原点O的抛物线C1与双曲线C2:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)都过点M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),且它们有共同的一个焦点F.则双曲线C2的离心率是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
19.在平面直角坐标系中,若$\left\{\begin{array}{l}{x≤2}\\{|y-2|≤x}\end{array}\right.$,则(x+1)2+y2的取值范围是( )
| A. | [$\sqrt{5}$,5] | B. | [$\frac{3\sqrt{2}}{2}$,5] | C. | [$\frac{9}{2}$,25] | D. | [9,25] |
16.执行如图所示的程序框图,若a=7.则输出的S=( )
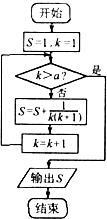

| A. | $\frac{6}{7}$ | B. | $\frac{15}{8}$ | C. | $\frac{13}{7}$ | D. | $\frac{11}{6}$ |