题目内容
4.某中学校本课程开设了A,B,C,D共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生.(Ⅰ)求在D课程没有被选中的条件下,A课程被甲选中的概率;
(Ⅱ)记“这3名学生选择A课程的人数”为X,求X的分布列和数学期望.
分析 (1)利用条件概率的概念求出n(E)=3×3×3=27,n(EF)=3×3=9,继而得出结论.
(2)两种方法处理此题,一种是常规的方法,一种是独立重复试验利用二项分布解题.
解答 解:(1)设“D课程没有被选中”为事件E,“甲选择了A课程”为事件F,
则n(E)=3×3×3=27,n(EF)=3×3=9,则P(E|F)=$\frac{n(EF)}{n(F)}=\frac{9}{27}=\frac{1}{3}$,
(2)解法一:X的所有可能取值为0,1,2,3,且
P(X=0)=$\frac{{3}^{3}}{{4}^{3}}=\frac{27}{64}$,P(X=1)=$\frac{{C}_{3}^{1}{3}^{2}}{{4}^{3}}=\frac{27}{64}$,
P(X=2)$\frac{{C}_{3}^{2}}{{4}^{3}}=\frac{9}{64}$,P(X=3)=$\frac{{C}_{3}^{3}}{{4}^{3}}=\frac{1}{64}$
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
解法二:因为A选修课被每位同学选中的概率均为$\frac{1}{4}$,没被选中的概率均为$\frac{3}{4}$,
所以X的所有可能取值为0,1,2,3,且X~B(3,$\frac{1}{4}$)
P(X=0)=($\frac{3}{4}$)3=$\frac{27}{64}$,P(X=1)=${C}_{3}^{1}×\frac{1}{4}×(\frac{3}{4})^{2}=\frac{27}{64}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{4})^{2}×\frac{3}{4}=\frac{9}{64}$,P(X=3)=($\frac{1}{4}$)3=$\frac{1}{64}$
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
点评 本题主要考查了条件概率的求解方法和独立重复试验的思路,属常考题型.

练习册系列答案
相关题目
12.已知顶点为坐标原点O的抛物线C1与双曲线C2:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)都过点M($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),且它们有共同的一个焦点F.则双曲线C2的离心率是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
19.在平面直角坐标系中,若$\left\{\begin{array}{l}{x≤2}\\{|y-2|≤x}\end{array}\right.$,则(x+1)2+y2的取值范围是( )
| A. | [$\sqrt{5}$,5] | B. | [$\frac{3\sqrt{2}}{2}$,5] | C. | [$\frac{9}{2}$,25] | D. | [9,25] |
16.执行如图所示的程序框图,若a=7.则输出的S=( )
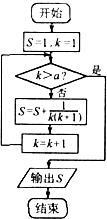

| A. | $\frac{6}{7}$ | B. | $\frac{15}{8}$ | C. | $\frac{13}{7}$ | D. | $\frac{11}{6}$ |
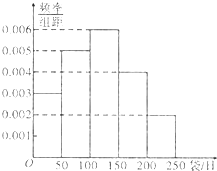 如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
如图所示的是某母婴用品专卖店根据以往销售奶粉的销售记录绘制的日销售量的频率分布直方图.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.