题目内容
7.已知数列{an}有a1=a,a2=p(常数p>0),对任意的正整数n,Sn=a1+a2+…+an,并有Sn满足Sn=$\frac{n({a}_{n}-{a}_{1})}{2}$.(1)求a的值;
(2)试确定数列{an}是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)对于数列{bn},假如存在一个常数b使得对任意的正整数n都有bn<b,且$\underset{lim}{n→∞}$bn=b,则称b为数列{bn}的“上渐近值”,令pn=$\frac{{S}_{n+2}}{{S}_{n+1}}$+$\frac{{S}_{n+1}}{{S}_{n+2}}$,求数列{p1+p2+…+pn-2n}的“上渐近值”.
分析 (1)通过在Sn=$\frac{n({a}_{n}-{a}_{1})}{2}$中令n=1计算即得结论;
(2)通过an=Sn-Sn-1计算可知an=$\frac{n-1}{n-2}$an-1,累乘即得结论;
(3)通过(2)可知Sn=$\frac{n(n-1)p}{2}$,进而裂项可知pn=2+2($\frac{1}{n}$-$\frac{1}{n+2}$),并项相加、取极限即得结论.
解答 解:(1)∵Sn=$\frac{n({a}_{n}-{a}_{1})}{2}$,
∴a1=$\frac{{a}_{1}-{a}_{1}}{2}$=0,
∴a1=a=0;
(2)由(1)可知an=Sn-Sn-1=$\frac{n{a}_{n}-(n-1){a}_{n-1}}{2}$,
∴an=$\frac{n-1}{n-2}$an-1,
∴an=$\frac{n-1}{n-2}$•$\frac{n-2}{n-3}$•…•$\frac{3}{2}$•$\frac{2}{1}$•a2=(n-1)p,
∴数列{an}是以0为首项、p为公差的等差数列;
(3)由(2)可知Sn=$\frac{n({a}_{n}-{a}_{1})}{2}$=$\frac{n(n-1)p}{2}$,
∴pn=$\frac{{S}_{n+2}}{{S}_{n+1}}$+$\frac{{S}_{n+1}}{{S}_{n+2}}$=$\frac{n+2}{n}$+$\frac{n}{n+2}$=2+2($\frac{1}{n}$-$\frac{1}{n+2}$),
∴p1+p2+…+pn-2n=2(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n-1}$-$\frac{1}{n+1}$+$\frac{1}{n}$-$\frac{1}{n+2}$)
=2(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=3-2($\frac{1}{n+1}$+$\frac{1}{n+2}$)
<3,
∵$\underset{lim}{n→∞}$(p1+p2+…+pn-2n)=3,
∴数列{p1+p2+…+pn-2n}的“上渐近值”为3.
点评 本题是一道数列与不等式的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

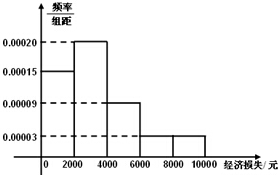 2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图(如图):
2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图(如图):表一:
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款低于500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
(Ⅱ)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50居民捐款情况如表1,在表1表格空白处填写正确数字,并说明是否有95%以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(Ⅲ)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,有2天李师傅比张师傅早到小区的概率.
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |