题目内容
12.已知数列{an},满足a1=2,an+1=$\frac{{a}_{n}}{2}$+$\frac{1}{{a}_{n}}$,求证:1<an<$\frac{3}{2}$+$\frac{1}{n}$.分析 由题意可知an>0,把原递推式化为$\frac{1}{2}$an2-an+1an+1=0,由△≥0得到${a}_{n}>\sqrt{2}>1$,然后利用数学归纳法证明an<$\frac{3}{2}$+$\frac{1}{n}$.
解答 证明:∵a1=2,an+1=$\frac{{a}_{n}}{2}$+$\frac{1}{{a}_{n}}$,∴an>0,
由an+1=$\frac{{a}_{n}}{2}$+$\frac{1}{{a}_{n}}$,得$\frac{1}{2}$an2-an+1an+1=0,由△=an+12-2≥0,得${a}_{n+1}≤-\sqrt{2}$(舍去)或${a}_{n+1}≥\sqrt{2}$,
则an>1.
当n=1时,a1=2<$\sqrt{2}$+1$<\frac{3}{2}+1$;
当n=2时,a2=$\frac{1}{2}{a}_{1}+\frac{1}{{a}_{1}}$=$\frac{3}{2}$<$\sqrt{2}$+$\frac{1}{2}$$<\frac{3}{2}+\frac{1}{2}$.
假设当n=k(k∈N*)时,ak<$\sqrt{2}+\frac{1}{k}$$<\frac{3}{2}+\frac{1}{k}$,
那么当n=k+1时,${a}_{k+1}=\frac{1}{2}{a}_{k}+\frac{1}{{a}_{k}}$,
∵$\frac{1}{2}{a}_{k}+\frac{1}{{a}_{k}}≥\sqrt{2}$,当且仅当${a}_{k}=\sqrt{2}$时等号成立,$\sqrt{2}$≤ak<$\sqrt{2}$+$\frac{1}{k}$,
∴${a}_{k+1}≤\frac{1}{2}$($\sqrt{2}+\frac{1}{k}$)+$\frac{1}{\sqrt{2}+\frac{1}{k}}$.
下面用作商法比较$\frac{1}{2}$($\sqrt{2}+\frac{1}{k}$)+$\frac{1}{\sqrt{2}+\frac{1}{k}}$和$\sqrt{2}$+$\frac{1}{k+1}$的大小.
∵$\frac{\frac{1}{2}(\sqrt{2}+\frac{1}{k})+\frac{1}{\sqrt{2}+\frac{1}{k}}}{\sqrt{2}+\frac{1}{k+1}}$=$\frac{\frac{4{k}^{2}+2\sqrt{2}k+1}{2k(\sqrt{2}k+1)}}{\frac{\sqrt{2}k+\sqrt{2}+1}{k+1}}$=$\frac{4{k}^{3}+(4+2\sqrt{2}){k}^{2}+(2\sqrt{2}+1)k+1}{4{k}^{3}+4(1+\sqrt{2}){k}^{2}+2(\sqrt{2}+1)k}$<1,
∴$\frac{1}{2}$($\sqrt{2}+\frac{1}{k}$)+$\frac{1}{\sqrt{2}+\frac{1}{k}}$<$\sqrt{2}$+$\frac{1}{k+1}$,
∴${a}_{k+1}<\sqrt{2}+\frac{1}{k+1}<\frac{3}{2}+\frac{1}{k+1}$,
即当n=k+1时,an<$\frac{3}{2}$+$\frac{1}{n}$成立.
综上an<$\frac{3}{2}$+$\frac{1}{n}$.
∴1<an<$\frac{3}{2}$+$\frac{1}{n}$.
点评 本题考查数列递推式,考查了数学归纳法证明数列不等式,利用归纳法证明与自然数有关的命题时,中间可穿插分析法,作商法等数学方法,是中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 1+i | B. | -1+i | C. | $\sqrt{2}$ | D. | 2 |
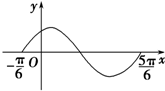 如图是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象,将该图象向右平移m(m>0)个单位后,所得图象关于直线x=$\frac{π}{4}$对称,则m的最小值为( )
如图是函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)在区间[-$\frac{π}{6}$,$\frac{5π}{6}$]上的图象,将该图象向右平移m(m>0)个单位后,所得图象关于直线x=$\frac{π}{4}$对称,则m的最小值为( )| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
| A. | [-4,0] | B. | [0,4] | C. | [-2,4] | D. | [-4,4] |